運動論磁気リコネクション¶

著者:: 銭谷誠司（国立天文台）

はじめに¶

磁気リコネクションは、プラズマ中で磁力線が繋ぎ変わり、磁気エネルギーをプラズマのエネルギーとして解放する素過程である。磁力線が反転するというアイデアは、太陽フレアでの粒子加速に関連して1940年代に提案された（ Giovanelli, 1946 ）。この考えは、1950年代に洗練されていき、地球磁気圏周辺で磁力線が繋ぎ変わることが議論されるようになった（ Dungey, 1961 ）。本格的なリコネクション研究の幕開けは、1950〜60年代にかけて構築された MHD 理論モデルであろう（ Sweet, 1958 ; Parker, 1957 ; Petschek, 1964 ）。こうした理論は、1970年代後半から MHD シミュレーションによって検証されていき、MHD の電気抵抗モデルとリコネクションの非線形発展との関係が明らかになってきた。また、1980〜90年代からはハイブリッド及び粒子シミュレーション研究が行われるようになり、MHD 近似で記述できない運動論効果が議論されるようになった。20世紀のリコネクション研究の象徴である GEM challenge（ Birn et al., 2001 ）では、Hall 効果の重要性を強調している。21世紀は粒子シミュレーションの大規模化がさらに進み、運動論３次元リコネクションも本格的に研究されるようになってきた。

基礎的な性質¶

概要¶

_images/mrx_theory1.png — リコネクション系の概要と座標系¶

リコネクション系の概要を上図に示す。インフロー領域の逆向き磁力線が、磁化したプラズマとともに中央に運ばれて、Ｘ点で繋ぎ変わる。繋ぎ変わった磁力線は張力でプラズマを加速し、高速のリコネクションジェットが下流に流れてゆく。このとき、上流側に蓄えられていた磁気エネルギーが、下流のプラズマエネルギー（ジェットのバルクエネルギー、熱エネルギー、そして非熱的粒子エネルギー）として解放される。上流や下流では概ね理想 MHD 近似が成り立っているが、Ｘ点周辺の磁気拡散領域では、プラズマ理想条件 $\bf{E}+(\bf{V}/c)\times\bf{B}=0$ が破れて、MHD近似外の物理（運動論効果）が重要になってくる。特徴的な領域の名称と性質を簡単にまとめておく。

インフロー／上流領域¶: リコネクション領域に磁場・プラズマを供給する。概ね理想 MHD 近似が成り立っている。地球磁気圏尾部に限って、リコネクションの上流領域をローブと呼ぶこともある。
Ｘ点／X-line／リコネクション点¶: 磁力線が繋ぎ変わる点。英語では X-line あるいは X-point であるが、３次元計算が行われている現在では X-line と呼ぶ方が良いだろう。日本語では X-ray と紛らわしいので「Ｘ線」という言い方はしない。
磁気拡散領域／磁気散逸領域¶: Ｘ点周辺の重要領域（灰色）で、この領域の構造と内部で起きる散逸過程はリコネクション物理の最重要問題である。プラズマ理想条件は成立していない。運動論プラズマでは磁気拡散領域の定義自体が論争テーマになっている。
セパラトリックス¶: 上流側と下流側の磁気トポロジーの境界（青の点線）。あるいは上流の静止プラズマと下流のアウトフローを隔てる圧力・温度勾配のある境界層。後者の意味で使う場合は、厳密には磁気トポロジー境界とは一致しない。
アウトフロー／リコネクションジェット¶: リコネクション領域から下流側に吐き出される高速のプラズマ流。より大規模なアウトフロー構造を exhaust と呼ぶこともある。

pCANS では、コードの都合上、概要図右の (1) の座標系を採用している。これは太陽面のリコネクション研究で使われる座標系である。運動論リコネクションの理論研究では、磁力線を X 方向にとることが多い。例えば、(2) のようにリコネクションを XY 面で議論する座標系はよく使われている。これを "simulation coordinate" と称することもある。また、(3) のようにリコネクション面を XZ 面に設定すると、運動論研究が進んでいて、なおかつ長年の観測研究の蓄積がある地球磁気圏尾部の GSM 座標系と対応させることができる。さらに地球磁気圏昼側やマグネトシースのリコネクション観測研究では、(4) の LMN 座標系を使うことが多い。N は Minimum Variance Analysis で決まる法線（Normal）の方向である。以下の解説では pCANS の内部座標にあわせて (1) を使うが、理論・シミュレーションの発表では (2) か (3) のどちらかを使うことをお勧めする。

アウトフロー速度¶

_images/mrx_theory2.png — リコネクション領域の概念図¶

上図 (a)のように磁気拡散領域の大きさを $L \times \delta$ とする。この中身はブラックボックスで理想 MHD 近似を使うことはできない。しかし、外側では概ね MHD 近似が成り立っているから、保存形 MHD 方程式を用いてエネルギー収支を考えることができる。以下、添字の $in$ , $out$ は、インフロー／アウトフロー領域の物理量を意味する。リコネクションが準定常（ $\partial/\partial t=0$ ）に達したとき、磁気拡散領域に流入／流出する物理量（磁力線フラックス、質量、エネルギー）の釣り合いを考えると

(1)¶ $B_{in}v_{in} = B_{out}v_{out}$

(2)¶ $\rho_{in} L v_{in} = \rho_{out} \delta v_{out}$

(3)¶ $\left( \frac{1}{2} \rho_{in}v^2_{in} + \frac{\gamma}{\gamma-1} p_{in} + \frac{B_{in}^2}{4\pi} \right) L v_{in} = \left( \frac{1}{2} \rho_{out}v^2_{out} + \frac{\gamma}{\gamma-1} p_{out} + \frac{B_{out}^2}{4\pi} \right) \delta v_{out}$

が成り立つ。 $\gamma=5/3$ は比熱比である。流入するエネルギーはほぼ Poynting flux、流出するエネルギーは主にプラズマ（バルクの運動エネルギーとエンタルピーフラックス）であるとして、エネルギー収支を簡略化すると

(4)¶ $\frac{B_{in}^2}{4\pi} L v_{in} \approx \left( \frac{1}{2} \rho_{out}v^2_{out} + \frac{\gamma}{\gamma-1} p_{out} \right) \delta v_{out}$

である。流出エネルギーの２項めは、プラズマのエンタルピーフラックス（内部エネルギーの流れ＋外部に対してする仕事）である。この項は、通常の Sweet-Parker 理論では考慮されていないことに注意する。

簡単のため、磁気エネルギーがバルクエネルギーとエンタルピーフラックスに等分配されると仮定して、

(5)¶ $\frac{B_{in}^2}{4\pi} L v_{in} \approx \left( \rho_{out}v^2_{out} \right) \delta v_{out}$

これと連続方程式より

(6)¶ $v_{out} \approx c_{A,in} = \frac{B_{in}}{\sqrt{4\pi\rho_{in}}}$

となり、リコネクションのアウトフロー速度は、ほぼ上流Alfven速度 $c_{A,in}$ であることがわかる。ここで先ほどの等分配の仮定を検証してみよう。アウトフロー領域で縦方向の圧力バランスを考えると、プラズマ圧は上流側の磁気圧と釣り合うから

(7)¶ $p_{out} \sim \frac{ B_{in}^2 }{ 8\pi }.$

となる。これでエンタルピーフラックス項を評価すると、

(8)¶ $\left(\frac{\gamma}{\gamma-1} p_{out} \right) \delta v_{out} \sim \left( \frac{\gamma}{\gamma-1} \frac{\rho_{in}}{\rho_{out}} \right) \left( \frac{1}{2} {\rho_{out}} c^2_{A,in} \right) \delta v_{out}$

となる。筆者の経験では、リコネクションの圧縮率 $({\rho_{out}}/{\rho_{in}})$ は２倍程度で、このとき右辺の係数も $({\gamma}/[\gamma-1]) ({\rho_{in}}/{\rho_{out}}) \sim 1$ であり、エンタルピーフラックスがAlfven速度のバルクエネルギー流と同程度になることがわかる。一般的には、エンタルピーフラックスがやや大きくなり、 $v_{out} < c_{A,in}$ となることが多い。 (6) 式はアウトフロー速度の理論的上限と考えれば良いだろう。

以上の議論は、近年の理論モデル（ Cassak & Shay, 2007 ; Birn et al., 2010 ; Hesse et al., 2011 ）を筆者なりに簡略化したものである。Sweet-Parker, Petschek を含むさまざまなリコネクション理論も $v_{out} \sim c_{A,in}$ という点で一致している。

リコネクションレート¶

もうひとつ、リコネクションを特徴づける重要パラメーターがリコネクションレート（Reconnection rate）で、Ｘ点を越えて磁束が輸送される効率を表す。前節で説明したAlfvenicなアウトフローは、ほとんどのリコネクションで普遍的に見られる。しかし、リコネクションのタイプによってリコネクションレートは異なる。

２次元リコネクションでは、リコネクションレートはＸ点の電場の垂直成分 $E_z = E_{rec}$ で表すことが多い。この $E_{rec}$ をリコネクション電場と呼ぶ。リコネクションの概念図 (b) のようなＸ点と無限遠を結ぶ閉曲線を考え、遠方のプラズマが静止している（ ${\bf E}=-({\bf V}/c)\times{\bf B}=0$ ）とすると、ファラデーの法則

(9)¶ $\oint {\bf E} \cdot ds = -\frac{1}{c} \frac{d}{dt} \Phi$

から、 $E_{rec}$ が（リコネクションによって運ばれた）磁束の変化率を表すことがわかる。よく発達したリコネクションでは、磁気拡散領域周辺では $E_z$ はほぼ一様である。このことは、準定常・２次元（ $\partial/\partial t=0$ , $\partial/\partial z=0$ ）のとき、ファラデーの法則の微分形 $({\partial}/{\partial t})\bf{B} = - c \nabla \times \bf{E}$ から $E_z = E_{rec} = {\rm const.}$ となることからわかる。Ｘ点だけでなく、磁気拡散領域周辺の $E_z \sim E_{rec}$ を総称してリコネクション電場と呼ぶ。

このリコネクション電場 $E_{rec}$ を上流の物理量を用いて

(10)¶ $\mathcal{R} := \frac{cE_{rec}}{c_{A,in}B_{in}}$

と規格化したものがリコネクションレート $\mathcal{R}$ である。上流では理想MHD近似が成り立つから

(11)¶ $\mathcal{R} \approx (v_{in}/c_{A,in})$

となり、アウトフロー速度の上限 $c_{A,in}$ に対するインフロー速度 $v_{in}$ の Mach number と考えることができる。リコネクションが上流から吸い込む磁気エネルギーは $\frac{1}{4\pi}B_{in}^2L~v_{in} \propto v_{in} \propto \mathcal{R}$ であるから、 $\mathcal{R}$ は系のエネルギー変換効率の指標とも言える。さらに $v_{out} \approx c_{A,in}$ に達したとき、

(12)¶ $\mathcal{R} \approx (v_{in}/c_{A,in}) \approx (v_{in}/v_{out}) \approx (B_{out}/B_{in})$

となり、 $\mathcal{R}$ はインフローとアウトフローの速度比、あるいは磁場の比率（ $\approx$ セパラトリックスの傾き角）に相当する。運動論リコネクションのリコネクションレートは $\mathcal{R} \sim 0.1$ であることが知られており、この値 $\mathcal{R} \sim 0.1$ は "Universal reconnection rate" とも呼ばれる。リコネクションレートが $0.1$ に落ち着く理由はわかっておらず、リコネクション理論の最重要問題の１つである。

ところで、リコネクションレートの定義には、式 (10) の他にもいくつか流儀がある。2000年代前半の研究では、典型磁場 $B_0$ と典型Alfven速度 $c_{A0}$ を用いて $\mathcal{R} := {cE_{rec}}/({c_{A0}B_{0}})$ とすることもあった。このときは必ずしも $c_{A0} = c_{A,in}$ でない。また、リコネクションレートを直接 $\mathcal{R} = v_{in}/v_{out}$ とする流儀もあるが、この方法は避けるべきだろう。何らかの理由でアウトフローがせき止められた場合にも、レートが大きく見えてしまうからである。さらに３次元では、リコネクション領域が乱流的な構造になってしまうために、 $E_{rec}$ のような便利な量は存在せず、研究者が試行錯誤している段階である。

課題設定¶

Harris 平衡解¶

リコネクション問題は、通常、Harris 解（ Harris, 1962 ）と呼ばれるモデルから出発する。ここでは pCANS の座標系にあわせて、磁場やプラズマ密度が x 方向に変化していると仮定する。磁場は 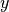$y$ 成分が $-B_0$ から $+B_0$ に変化する。 $z$ 方向は ${\partial}/{\partial z}=0$ で、磁場反転を担う電流が $z$ 方向を向いている。

導出は原論文（ Harris, 1962 ）に譲るとして、イオン、電子（ $s=i,e$ ）それぞれについて、一様温度 $T_s$ 、ドリフト速度 $V_s$ の Shifted-Maxwell 分布を考える。

(13)¶ ${\bf B}(x) &= B_{0} \tanh(x/L) {\bf e}_y \\ f_s(x) &= n_{0} \cosh^{-2}(x/L) \left(\frac{m_s}{2\pi T_s}\right)^{3/2}\exp\left(-\frac{m_s(v^2_x+v^2_y+(v_z-V_s)^2)}{2T_s}\right)$

ここで $L$ は電流層の幅で、密度は $n_s(z) = n_{0} \cosh^{-2}(x/L)$ となる。

そして $L, V, T$ を

(14)¶ $-\frac{V_i}{V_e} = \frac{T_i}{T_e} \\ L = \frac{2(T_i+T_e)}{B_0|V_i-V_e|}$

を満たすようにとると、プラズマ分布関数は厳密平衡解になる。得られた解は圧力バランスとアンペールの法則

$n_{0}(T_i+T_e) &= \frac{B_0^2}{8\pi} \\ e n_{0}(V_i-V_e) &= \frac{B_0}{4\pi L}$

を満たしている。また、式 (13) を無衝突ボルツマン方程式

$\frac{\partial}{\partial t} f_s+ {\bf v} \cdot \nabla f_s+ \frac{q_sn_s(x)}{m_s}({\bf E}+\frac{\bf v}{c}\times{\bf B}) \cdot \nabla_{\bf v} f_s = 0$

に代入すると、 $({\partial}/{\partial t}) f_s = 0$ であることがわかる。電荷 $q_s$ は $q_i=e$ , $q_e=-e$ である。

Harris 解には、電流方向の一様の磁場（ガイド磁場という）や一様の背景プラズマを加えることができる。元の解にこれらの成分を重ねても平衡条件を保っている。

(15)¶ ${\bf B}_{\rm add}(x) &= B_{z0} ~ {\bf e}_z \\ f_{s,{\rm add}}(z) &= n_{bg} \left(\frac{m_s}{2\pi T_{bg,s}}\right)^{3/2} \exp\left(-\frac{m_s {\bf v}^2}{2T_{bg,s}}\right)$

ガイド磁場の強さ $B_{z0}$ や背景プラズマの温度 $T_{bg,s}$ 、背景プラズマ密度 $n_{bg}$ （ただし $n_{bg}=n_{bg,i}=n_{bg,e}$ ）はフリーパラメーターである。Harrisシートの無限遠方（ $x \rightarrow \pm \infty$ ）は密度がゼロだが、自然界ではある程度プラズマが存在しているから、一定密度の背景プラズマ $n_{bg}$ （ $n_{bg} < n_0$ ）を追加することが多い。

ところで、自然界の電流層が Harris 解で記述できるかは自明ではない。Harris 解の電流方向のモーメント密度 $M_z$ は

$M_z(x) = n_0 \cosh^{-2}(x/L) \cdot \sum_{s=i,e} m_s V_s$

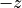である。イオンと電子の温度比 $T_i/T_e$ はフリーパラメーターである。熱平衡状態では $T_i = T_e$ となるべきだが、地球磁気圏のプラズマシートでイオンが高温であることを根拠に $T_i/T_e = 5$ とすることも多い。 $T_i/T_e$ 中性拘束条件（式 (14) ）は $-(V_i/V_e)=(T_i/T_e)>1$ を意味し、そもそも $m_i>m_e$ であるから、モーメントの大半を $-z$ 向きのイオンが担っている。また、電流層が薄いときのイオンドリフト速度 $V_i$ は、系の典型アルフベン速度 $c_A$ に達することもある。リコネクションジェットの最大速度が $\mathcal{O}(c_A)$ であるのに、初期ドリフト速度が $\mathcal{O}(c_A)$ で、大きなモーメントを担っている。リコネクション系の力学を議論するときには、こうした「不自然な」事実にも注意する必要がある。

ともあれ、上で述べた通り、簡単にガイド磁場や背景プラズマを追加できるうえ、磁気島の周期構造を取り込んだFadeev解、磁気圏尾部研究で使われる２次元拡張、Harris-Hoh相対論解など、さまざまな発展形も存在する。Harris解が運動論リコネクション研究の出発点であることは間違いない。

背景プラズマの扱い¶

Harris 解に背景プラズマ成分を追加すると、ion-ion kink 不安定という人工的な不安定が起きることが知られている（ Daughton, 1999 ）。ion-ion kink 不安定は 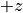$+z$ 方向にドリフトするHarris解イオン（ (13) ）と静止した背景イオン（ (15) ）が相互作用して起きる不安定で、電流方向（ $z$ 方向）に波数を持つ。ion-ion kink 不安定を防ぐためには、以下の２通りの方法が使われている。

１つめは理論家に多い方法で、電流層と背景の２成分プラズマを１つのプラズマ成分と考える方法である。温度を一定にし（ $T_i = T_{bg,i}$ , $T_e = T_{bg,e}$ ）、プラズマ密度および電流プロファイル

(16)¶ $n_{\rm total}(x) &= n_{0} \cosh^{-2}(x/L) + n_{bg} \\ J(x) &= J_{0} \cosh^{-2}(x/L)$

を使って、ドリフト速度を

(17)¶ $V(x) \propto J_z(x) / n_{\rm total}(x)$

と定義し直す。そして、式 (16) , (17) 、一定の温度 $T_s$ を使って、１成分のプラズマをshifted Maxwell分布で初期化する。

(18)¶ $f_s(x) = n_{\rm total}(x) \left(\frac{m_s}{2\pi T_s}\right)^{3/2}\exp\left(-\frac{m_s(v^2_x+v^2_y+(v_z-V_s(x))^2)}{2T_s}\right)$

このとき、プラズマは厳密な平衡条件を満たしていないことに注意する。

２つめは地球磁気圏の研究グループがよく使う方法である。Harris解に重ね合わせる背景プラズマの密度（式 (15) ）を

(19)¶ $n_{bg}(x) = n_{bg0} [1-\cosh^{-2}(x/L)]$

のようにして、電流層内から背景プラズマを取り除く。この方法も平衡を満たさず、x 方向の圧力バランスも崩してしまうが、上流プラズマは低密度・低温で圧力が小さいことが多いため、リコネクション系の進化にはあまり影響しない。

ion-ion kink 不安定は $z$ 方向に波数を持つ不安定であり、 $(\partial/\partial z)=0$ の２次元シミュレーションでは顕在化しない。しかし、電流層中に２成分のプラズマが混在することは物理的直感に反するから、２次元シミュレーションでも対処しておくと良い。

トリガー方法¶

電流シート構造で粒子シミュレーションを行うと、テアリング不安定という不安定が発生して磁気リコネクションを引き起こす。プラズマシートの厚み（や粒子数・コードの性質）にも依るが、リコネクションが起きるまでの時間は意外と長く、計算コストも馬鹿にならない。また、リコネクションの起きる位置がわからないうえに、複数のリコネクションが同時に発生することもあって、１つのリコネクション領域にフォーカスできない。そこで、電流シートに小さな外部擾乱を与えて、無理矢理リコネクションを起こすことを考える。

よく用いられるのは、ベクトルポテンシャルに小さな擾乱 $\delta A_z$ を与えて、磁場を修正する方法である。

(20)¶ $(\delta B_x, \delta B_y) = (\partial_y \delta A_z, -\partial_x \delta A_z)$

例えば、GEM Challenge（ Birn et al, 2001 ）では

(21)¶ $\delta A_z(x,y) = A_0 \cos(\pi x/L_x) \cos(2\pi y/L_y)$

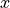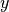という形の擾乱を与えている。 $L_x$ , $L_y$ は $x$ , $y$ 方向のシステムサイズである。GEM 形の擾乱は、擾乱磁場がプラズマの上流領域にも広がるうえ、系のサイズが大きくなるとリコネクションの成長が遅くなるため、あまりお勧めできない。筆者がお勧めするのは、リコネクション点にローカライズした擾乱

(22)¶ $\delta A_z(x,y) = 2L B_1 \exp[-(x^2+y^2)/(2L)^2]$

である（ Zenitani et al., 2011 ）。粒子シミュレーションでは、擾乱磁場の強さを $B_1/B_0 \sim 10\%$ のオーダーに設定すると、比較的早くリコネクションを引き起こすことができる。

こうした擾乱の形は、コードの性質や扱う問題によっていろいろ工夫することができる。MHD シミュレーションでは擾乱磁場は数 $\%$ 程度で十分である。

pCANS の設定¶

長年、運動論リコネクション研究が行われていた地球磁気圏プラズマシートでは、 $T_i > T_e$ , $L$ はイオン慣性長 $d_i=c/\omega_{pi}$ 程度であることが衛星観測でわかっている。 $T_i > T_e$ となる理由はわかっていないが、 $L \sim O(d_i)$ はHall効果の影響が出始めるスケールだから、運動論物理を見るにはちょうど良い。そこで、 pCANS では

$n_{bg}/n_0 &= 0.2 \\ T_e/T_i &= \alpha = 0.2 \\ L/d_i &= 0.5 \\ m_i/m_e &= 16 \\ \omega_{pe}/\Omega_{ce} &= 2$

とした。 $\omega_{pe}=(4\pi e^2n_0/m_e)^{1/2}$ はプラズマ振動数、 $\Omega_{ce}=(eB_0/m_ec)$ はジャイロ振動数である。グリッドサイズはデバイ長

(23)¶ $\Delta = \frac{1}{\sqrt{2}}\frac{v_{Te}}{\omega_{pe}}$

とした。分布関数は、電流層プラズマと背景プラズマを１成分にまとめて考え、式 (18) で初期化する。また、式 (22) のポテンシャルでリコネクションをトリガーする。

結果¶

_images/mrx_result1.png — **pCANS** の実行結果（ $\Omega_{ci}t=12.35$ ）。(a) イオン速度 ( $V_{iy}/c_{A0}$ )、 (b) 電子速度 ( $V_{ey}/c_{A0}$ ) (c) Hall 磁場 ( $B_{z}/B_{0}$ ) (d) イオンの理想条件（ $[\boldsymbol{E}+(\boldsymbol{V}_i/c)\times\boldsymbol{B}]_z/B_0$ ）を示す。¶

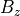上図は pCANS のデフォルト設定の実行結果で、 $\Omega_{ci}t=12.35$ での物理量を表している。イオンと電子がそれぞれ、中心のリコネクション点から上下に吹き出していることがわかる（上図 (a),(b)）。よく見ると、電子のジェットの方が高速である。また、電流シートの周辺から、リコネクション点に戻るリターンフローも見えるなど、より小さな構造を形成していることがわかる。このようなイオンと電子の流れの差によって、面内に電流ループができるため、磁場の紙面垂直成分（ $B_z$ ）が作られている（上図 (c)）。これらの結果を、ほぼ同じサイズの計算結果（例えば Pritchet, 2001 ）と比較してみると良いだろう。最後に示すのは、イオンの Ohm の法則 ${\bf E}+({\bf V}_i/c)\times{\bf B}$ の垂直成分（ $z$ 成分）である。中央の磁気拡散領域付近では、理想MHD近似 ${\bf E}+({\bf V}_{i}/c)\times{\bf B}=0$ （ ${\bf V}_{mhd}\approx {\bf V}_i$ ）が破れていることに注目する。磁気拡散領域周辺では、複雑な運動論効果が実効的な電気抵抗として働いて、磁力線を運ぶリコネクション電場を支えている。

_images/mrx_recrate.png — リコネクションレートの長期発展（ Zenitani et al., 2011 から転用）¶

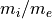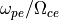比較のため、計算領域を一回り大きくしたシミュレーション結果（ $76.8 \times 38.4 [d_i]$ ）を紹介する。上図は、上流物理量で規格化したリコネクションレート（式 (10) ）の時間発展である。システムサイズが有限の場合、リコネクションの進行にともなって上流の磁場や密度が減っていくため、リコネクション電場 $E_z = E_{rec}$ も小さくなっていく。このことを考慮して、ここではリコネクションレートを、そのときそのときの上流の $c_{A,in}B_{in}$ の値を使って規格化した。規格化されたリコネクションレートは、ピークに達した後、〜0.1 の一定値に収束していることがわかる。多くの研究では、リコネクションは、質量比 $m_i/m_e$ , $\omega_{pe}/\Omega_{ce}$ などのパラメーターに依存せず、イオンで規格化した時間スケール（ $\Omega_{ci}^{-1}$ ）で進むことが知られている。演習課題では最初のピークぐらいまでしか見えないかもしれないが、余力があれば計算領域を大きくして長期発展を追ってみよう。

_images/mrx_3d.png — 磁力線の３次元構造（ Zenitani et al., 2011 から転用）¶

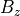上図は、質量比 $m_i/m_e=100$ , $\omega_{pe}/\Omega_{ce}=4$ のシミュレーション結果を pCANS の座標系で表したものである。Hall効果によって磁力線が手前側に曲げられて、紙面垂直方向の磁場成分（ $B_z$ ）が出来ているのが見える。 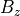$B_z$ はリコネクション点を中心に四重極構造を形成する（ Sonnerup, 1979 ）。この四重極磁場はHall磁場と呼ばれており、地球磁気圏リコネクションの衛星観測でも見つかっている。

計算量について¶

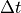上図でも示したように、リコネクションは大局的には $\Omega_{ci}^{-1}$ のタイムスケールで進行する。一方、電子のプラズマ振動を扱うため、粒子を解き進める時間ステップ $\Delta t$ は概ね $\omega_{pe}^{-1}$ に比例する。両者の時間スケールの差は

(24)¶ $\left(\frac{\omega_{pe}}{\Omega_{ci}}\right) \sim \left(\frac{\omega_{pe}}{\Omega_{ce}}\right)\left(\frac{m_i}{m_e}\right)$

倍である。

また、粒子シミュレーションの典型的なグリッドサイズはデバイ長 $\lambda_D \sim v_{Te}/\omega_{pe}$ である。リコネクションのような磁気エネルギー解放過程では、典型的な電子の熱速度 $v_{Te}$ は電子アルヴェン速度 $c_{A,e}$ に達するだろう。これに対して全体の空間サイズはイオン慣性長 $d_i$ であるから、両者のスケール差は１次元あたり

(25)¶ $\left(\frac{c}{\omega_{pi}}\right) \left(\frac{\omega_{pe}}{v_{Te}}\right) \sim \left(\frac{\omega_{pe}}{\omega_{pi}}\right)\left(\frac{c}{c_{A,e}}\right) \sim \left(\frac{m_i}{m_e}\right)^{1/2}\left(\frac{\omega_{pe}}{\Omega_{ce}}\right)$

倍である。１セルあたりの粒子数が同じ場合、空間 $N$ 次元の粒子シミュレーションの総計算量は、

(26)¶ $\left(\frac{m_i}{m_e}\right)^{(2+N)/2} \left(\frac{\omega_{pe}}{\Omega_{ce}}\right)^{1+N}$

に比例する。

2000年代の研究では $m_i/m_e=25$ がよく使われていた。実際、リコネクションレートやイオンスケールの構造は、質量比にはあまり依存しない。しかし、リコネクション領域の中に見える電子スケールの細かな構造はある程度、質量比に依存する。例えば、リコネクション点から吹き出す電子ジェット（ pCANS のデフォルト設定でも電子ジェットの形跡は見える）の厚みは電子慣性長 $d_e$ 以下である。イオン慣性長スケールの全体構造に対して、電子スケール構造は $(d_e/d_i) = (m_i/m_e)^{-1/2}$ 倍に比例して小さくなる。また、３次元系では、密度勾配のある領域でLower Hybrid Drift（LHD）不安定などのプラズマ不安定が起きるが、質量比 $m_i/m_e=100 - 200$ 以上で、現実世界と同じブランチのモードが立つことがわかってきている。

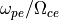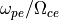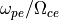振動数比 $\omega_{pe}/\Omega_{ce}$ は $2 - 4$ 程度の小さな値を用いる。上記のように $\omega_{pe}/\Omega_{ce}$ を小さくすると計算量を節約できるが、電子の物理を議論するときに注意しなければならない。例えば、電子の典型速度（電子アルヴェン速度）は $c_{Ae}/c = (\omega_{pe}/\Omega_{ce})^{-1}$ である。 $\omega_{pe}/\Omega_{ce} \approx 2$ のときは、ターゲット領域の電子がほぼ非相対論的電子で構成されているかどうか、分布関数を見て確認したほうが良いだろう（相対論的電子が混じることは問題ではないが、非相対論統計力学の解析手法が通用しなくなる）。また $\omega_{pe}/\Omega_{ce}$ をさらに大きくすると、デバイ長スケールの静電的乱流が見えるようになる（ Jara-Almonte et al., 2014 ）。電子熱速度〜電子典型速度〜電子アルヴェン速度のとき、 $\lambda_D \ll d_e \leftrightarrow \omega_{pe} \gg \Omega_{ce}$ のように、電子スケール構造（〜電子慣性長）とデバイ長が分離するからだと考えられる。このような微小擾乱のリコネクション系全体への影響はよくわかっていない。

展望¶

2010年代以降のメインテーマは、間違いなくリコネクション系の３次元発展であろう。プラズマ不安定があらゆる波数方向で成長できるため、これまで以上に複雑な構造が見える。例えば、セパラトリックス面が２次的テアリング不安定を起こして、乱流的にフラックスロープを生成するケースも報告されている（ Daughton et al., 2011 ）。また、非熱的粒子の起源である粒子加速問題（ Birn et al., 2012 , 2-3 章）や、リコネクションと乱流との関わり（ Lazarian & Vishniac, 1999 ）、そして、高エネルギー天体環境への応用（ Zenitani & Hoshino, 2007 ）なども重要な研究テーマである。