メインルーチン main.f¶
メインルーチン(ファイル main.f)は、大きく分けて「開始処理部(エピローグ)」「時間発展部」「終了処理部(エピローグ)」の3部構成からなる。さらにその前に、Fortranプログラムで必要な「配列定義部」がある。開始処理部では、サブルーチンmodelを呼び、メッシュ座標や初期条件を設定するのが主な動作である。時間発展部が主たる計算エンジンで、磁気流体方程式を解いて物理変数の時間発展を求める。与えられた終了条件をみたすまでこの部分が繰り返される。そして終了処理部では、終了メッセージを出力してプログラム実行を止める。以下、実際のプログラムにコメントを入れながら解説する。
c======================================================================|
c array definitions
c======================================================================|
implicit double precision (a-h,o-z)
! 倍精度浮動小数点データを基本データ型とする。
parameter (margin=1)
parameter (ix=1024+2*margin)
dimension x(ix),xm(ix),dx(ix),dxm(ix)
! x(*)がメッシュ座標、xm(*)はメッシュ境界の座標、dx(*)がメッシュ幅、dxm(*)はメッシュ中心間の距離。
! ixはx軸のメッシュ数
! marginは、興味ある領域の外に準備する、計算上必要な袖メッシュ数。計算エンジンに依存して数が異なる。ここで用いるmlw_mでは、1個。
dimension ro(ix),pr(ix)
dimension vx(ix),vy(ix),by(ix)
! 時間変化する基本変数の配列。roは密度、prは圧力、vx、vyは速度、byは磁場
dimension bx(ix),bxm(ix)
! x軸に沿った1次元MHDでは、磁場のx成分は時間変動しない(divB=0なので)。
! サブルーチンmodel.fで固定値として与えられる。
913 format (1x,' write ','step=',i8,' time=',e10.3,' nd =',i3)
915 format (1x,' stop ','step=',i8,' time=',e10.3)
c======================================================================|
c prologue
c======================================================================|
mcont=0
! mcont=1とすると、過去の計算結果データ(ディレクトリin/以下に置く)を読み込んで継続計算を実行する。
! 継続計算では、下のtendの値設定に注意すること。前回の計算の最終時刻がtendより大きいと、継続計算がただちに終了してしまう。
c----------------------------------------------------------------------|
c set parameters controling finalization and data-output
tend=0.1d0
! tendは終了させたい時刻。
nstop=100000
! nstopは終了させたいステージ数。
! t > tendまたはns>nstopが満たされたら計算終了。
dtout=0.01d0
! dtoutは、データ出力間隔。tの値がdtoutの(ほぼ)整数倍になったら出力。
c dtout=1.d-10
c nstop=1
c----------------------------------------------------------------------|
c initialize counters
merr = 0
ns = 0
t = 0.0d0
tp = 0.0d0
nd=1
mwflag=0
! 以上、カウンタの初期化。
! merrはエラーが起きたときゼロ以外の値が代入される。
! nsは計算ステージ数。
! tは時刻。tpは、ひとつ前のステージでの時刻。データ出力タイミングの判断に使う。
! ndは、次に出すデータが何番目か。
! mwflagは、「いま保持している計算結果を出力しました」というフラグ。重複して同じデータを出力するのを防ぐための仕掛け。
c----------------------------------------------------------------------|
c file open for "standart output"
mf_out=7
open(mf_out,file='out.txt',status='replace',iostat=merr)
if (merr.ne.0) then
merr=10001
goto 9999
endif
close(mf_out)
! 標準出力(コンソール出力)と同じ内容を残すファイル(out.txt)のオープン
! out.txtは出力のたびに開け閉めする。こうすると長時間の計算途中でも中身を確認できる。
c----------------------------------------------------------------------|
c file open
mf_params=9
call dacdefparam(mf_params,'params.txt')
! 計算パラメータを出力するファイル(params.txt)をオープン
mf_t =10
call dacdef0s(mf_t,'t.dac',6)
mf_ro=20
call dacdef1s(mf_ro,'ro.dac',6,ix)
mf_pr=21
call dacdef1s(mf_pr,'pr.dac',6,ix)
mf_vx=22
call dacdef1s(mf_vx,'vx.dac',6,ix)
mf_vy=23
call dacdef1s(mf_vy,'vy.dac',6,ix)
mf_by=24
call dacdef1s(mf_by,'by.dac',6,ix)
! 計算結果を出力するファイル(t.dac、ro.dac、pr.dacなど)をオープン
! 引数「6」は、データ型が倍精度であることを示す。
call dacputparami(mf_params,'ix',ix)
call dacputparami(mf_params,'margin',margin)
! 計算パラメータを出力
c----------------------------------------------------------------------|
c setup numerical model (grid, initial conditions, etc.)
call model(ro,pr,vx,vy,by,bx,bxm,gm,margin,x,ix,mf_params)
! メッシュ座標・初期条件を設定(後で詳述)
call grdrdy(dx,xm,dxm,x,ix)
! メッシュ座標(x)から、メッシュ幅(dx)やメッシュ境界での座標など(xm、dxm)を計算
call bnd(margin,ro,pr,vx,vy,by,ix)
! 境界条件の適用
c floor=1.d-9
c call chkdav(n_floor,ro,vx,floor,ix)
c call chkdav(n_floor,pr,vx,floor,ix)
c----------------------------------------------------------------------|
c read-data
ndi=1000
if (mcont.eq.1) then
mfi_t=60
call dacopnr0s(mfi_t,'in/t.dac',mtype,nx0)
mfi_ro=70
call dacopnr1s(mfi_ro,'in/ro.dac',mtype,ix0,nx0)
mfi_pr=71
call dacopnr1s(mfi_pr,'in/pr.dac',mtype,ix0,nx0)
mfi_vx=72
call dacopnr1s(mfi_vx,'in/vx.dac',mtype,ix0,nx0)
mfi_vy=73
call dacopnr1s(mfi_vy,'in/vy.dac',mtype,ix0,nx0)
mfi_by=74
call dacopnr1s(mfi_by,'in/by.dac',mtype,ix0,nx0)
do n=1,ndi
read(mfi_t,end=9900) t
read(mfi_ro) ro
read(mfi_pr) pr
read(mfi_vx) vx
read(mfi_vy) vy
read(mfi_by) by
enddo
9900 continue
! 以上、継続計算(mcont=1)のとき、過去の計算結果(ディレクトリin/の下に置く)を読み込む。
endif
c----------------------------------------------------------------------|
c data output
mf_x=11
call dacdef1d(mf_x,'x.dac',6,ix)
write(mf_x) x
close(mf_x)
mf_bx=12
call dacdef1d(mf_bx,'bx.dac',6,ix)
write(mf_bx) bx
close(mf_bx)
call dacputparamd(mf_params,'gm',gm)
write(mf_t) t
write(mf_ro) ro
write(mf_pr) pr
write(mf_vx) vx
write(mf_vy) vy
write(mf_by) by
write(6,913) ns,t,nd
open(mf_out,file='out.txt',status='old',form='formatted'
& ,position='append')
write(mf_out,913) ns,t,nd
close(mf_out)
nd=nd+1
! 初期条件を出力する
c======================================================================|
c time integration
c======================================================================|
1000 continue
ns = ns+1
mwflag=0
c----------------------------------------------------------------------|
c obtain time spacing
safety=1.0d0
dtmin=1.d-10
call cfl_m(dt,safety,dtmin,merr,gm,bx,ro,pr,vx,vy,by,dx,ix)
if (merr.ne.0) goto 9999
! CFL条件にもとづいて、時間刻み幅dtを各ステージで決定する。
! safetyは、CFL条件の臨界値から実際のdtを求めるときの安全係数。通常1以下の値。
! dtminは、dtの値に対する下限値。dt<dtminになるとエラーとみなして計算を止める。
tp = t
t = t+dt
! 時刻の更新
c----------------------------------------------------------------------|
c solve hydrodynamic equations
qav=1.d0
call mlw_m(ro,pr,vx,vy,by,bx,bxm,dt,qav,gm,dx,dxm,ix)
! 主要エンジン部。ここでは改良Lax-Wendroff(MLW)(とLapidus人工粘性)でMHD方程式を解く。
! qavは人工粘性の強さ。
call bnd(margin,ro,pr,vx,vy,by,ix)
! 境界条件の適用
c floor=1.d-9
c call chkdav(n_floor,ro,vx,floor,ix)
! 計算結果をチェックして、floorの値よりroが小さいメッシュでは値をfloorと置き換え、vxをゼロとする。
! この問題設定では不要。
c call chkdav(n_floor,pr,vx,floor,ix)
! 同様。ただしprをチェック。
c----------------------------------------------------------------------|
c data output
mw=0
nt1=int(tp/dtout)
nt2=int(t/dtout)
if (nt1.lt.nt2) mw=1
! 「dtoutの整数倍」の判断をする部分
if (mw.ne.0) then
write(mf_t) t
write(mf_ro) ro
write(mf_pr) pr
write(mf_vx) vx
write(mf_vy) vy
write(mf_by) by
write(6,913) ns,t,nd
open(mf_out,file='out.txt',status='old',form='formatted'
& ,position='append')
write(mf_out,913) ns,t,nd
close(mf_out)
nd=nd+1
mwflag=1
endif
! データ出力
c----------------------------------------------------------------------|
c loop test
if (ns .lt. nstop .and. t .lt. tend) goto 1000
! 主要計算部を繰り返すかどうかの判断文
! 「t<tendかつns<nstop」であれば繰り返す
c======================================================================|
c epilogue
c======================================================================|
9999 continue
c----------------------------------------------------------------------|
c data output
if (mwflag.eq.0) then
write(mf_t) t
write(mf_ro) ro
write(mf_pr) pr
write(mf_vx) vx
write(mf_vy) vy
write(mf_by) by
write(6,913) ns,t,nd
open(mf_out,file='out.txt',status='old',form='formatted'
& ,position='append')
write(mf_out,913) ns,t,nd
close(mf_out)
endif
! データ出力
c----------------------------------------------------------------------|
c ending message
write(6,915) ns,t
if (merr.eq.0) then
write(6,*) ' ### normal stop ###'
else
write(6,*) ' ### abnormal stop ###'
write(6,*) ' merr = ',merr
endif
open(mf_out,file='out.txt',status='old',form='formatted'
& ,position='append')
write(mf_out,915) ns,t
if (merr.eq.0) then
write(mf_out,*) ' ### normal stop ###'
else
write(mf_out,*) ' ### abnormal stop ###'
write(mf_out,*) ' merr = ',merr
endif
close(mf_out)
! 終了メッセージ
stop
! プログラム終了
end
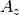 の等高線)で示される。
の等高線)で示される。