応用課題¶
| 著者: | 高橋博之 (国立天文台) |
|---|
モーメント法を用いた相対論的輻射流体の数値解法¶
近年のスーパーコンピュータの発達と数値計算コードの高精度化に伴い、より高解像度・長時間の磁気流体計算を行う事が可能になってきた。その一方で、磁気流体に自己重力や、特殊・一般相対性理論、電気抵抗、熱伝導、粘性、輻射輸送など、より多くの物理を含めた現実的な計算も行われている。この章では相対論的流体に輻射の効果を無矛盾に取り入れた相対論的輻射流体数値計算の紹介をする。輻射場は簡単のため、光子分布関数を運動量空間で積分したモーメント量(輻射エネルギー密度、フラックス)で記述する。モーメント方程式の導出は省略するが、詳しくは数値天文学マニュアル(http://www.astro.phys.s.chiba-u.ac.jp/hpci/ws2012/TechMan2012/)や Mihalas & Mihalas (1984), Kato et al. (2008) , Takahashi et al. (2013) を参照してほしい。
以下、メトリックは平坦とし( 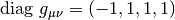 )、添字のギリシャ文字とアルファベットはそれぞれ時空4次元(
)、添字のギリシャ文字とアルファベットはそれぞれ時空4次元( 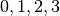 )と空間3次元
)と空間3次元 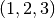 を表す。
を表す。
相対論的輻射流体方程式¶
相対論的輻射流体方程式は以下で記述される:
(1)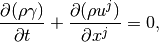
(2)![\frac{1}{c}\frac{\partial}{\partial t}
\left[(\epsilon + p_g)\gamma^2 - p_g\right]
+ \frac{\partial}{\partial x^j}
\left[(\epsilon + p_g)\gamma \frac{u^j}{c}\right]=
G^0,](_images/math/0045d255dca8c16cbcf8b50b7b09a0b10d28ea4b.png)
(3)![\frac{1}{c^2}\frac{\partial}{\partial t}
\left[(\epsilon + p_g)\gamma u^i \right]
+ \frac{\partial}{\partial x^j}
\left[(\epsilon + p_g)\frac{u^i u^j}{c^2} + \delta^{ij} p_g\right]=
G^i,](_images/math/ea05553ce6734138aa04b1a42be814a49c4b4dbb.png)
(4)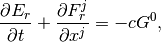
(5)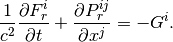
上から順に質量保存、ガスのエネルギー保存、ガスの運動量保存、輻射の0次モーメント式、輻射の1次モーメントの式を表す。 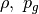 はガス密度、ガス圧で
はガス密度、ガス圧で 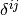 はクロネッカーデルタである。
はクロネッカーデルタである。  は静止質量エネルギー密度を含めた流体のエネルギー密度を表しており、polytropic関係を仮定すると内部エネルギー密度
は静止質量エネルギー密度を含めた流体のエネルギー密度を表しており、polytropic関係を仮定すると内部エネルギー密度  、比熱比
、比熱比 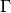 を用いて
を用いて
(6)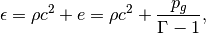
とかける。 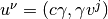 は流体4元速度で、3元速度
は流体4元速度で、3元速度 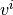 、ローレンツ因子
、ローレンツ因子 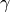 との間に
との間に 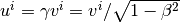 の関係がある。ただし
の関係がある。ただし 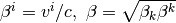 である。
である。
![E_r [\mathrm{erg\ cm^{-3}}],\ F_r^i [\mathrm{erg\ cm^{-2}\ s^{-1}}],\ P_r^{ij} [\mathrm{erg\ cm^{-3}}]](_images/math/1c1b3bcde8710d8a46810b5f9f9d963be4d406a0.png) はそれぞれ輻射場のエネルギー密度、フラックス、ストレスで、輻射とガスは輻射4元力密度
はそれぞれ輻射場のエネルギー密度、フラックス、ストレスで、輻射とガスは輻射4元力密度 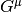 を通してエネルギー運動量のやり取りを行う。
を通してエネルギー運動量のやり取りを行う。
(7)![G^0 =-\frac{\rho\gamma \kappa_0}{c}
\left(4\pi \mathrm{B} - c E_r +\beta_j
F_r^j\right)
-\frac{\rho \gamma \sigma_0}{c}
\left[\frac{u^2 E_r}{c} + \frac{u_j u_k P_r^{jk}}{c}
- \left(2\gamma^2 - 1\right)\beta_jF_r^j
\right],](_images/math/9223f90a3e0d3cf15381fae1f7a4952154c90a91.png)
(8)![G^i = &-\frac{\rho \gamma \kappa_0}{c}
\left(4 \pi \mathrm{B} \beta^i - F^i_r +v_k P_r^{ik} \right) \\
&+\frac{\rho \gamma \sigma_0}{c}
\left[F_r^i - \gamma E_r u^i - v_k P_r^{ik}
+v^i\left(\frac{2 \gamma u_k F_r^k}{c^2}-\frac{u_j u_k P_r^{jk}}{c^2}\right)
\right].](_images/math/b674e79eef09ac9c57abc98137d373ad87ff1ced.png)
ただし 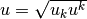 である。
である。 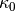 ,
, 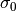 はそれぞれ共動座標系で評価した吸収係数、及び散乱係数(
はそれぞれ共動座標系で評価した吸収係数、及び散乱係数( 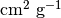 )を表す。
)を表す。 ![\mathrm{B} [\mathrm{erg\ cm^{-2}\ s^{-1}}]](_images/math/ee60d68274fa0e88e0013a730179b8fc86156c8c.png) は黒体輻射強度でガス温度を用いて
は黒体輻射強度でガス温度を用いて
(9)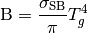
となる。ここで 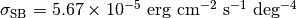 はStefan-Boltzmann定数である。このガス温度は状態方程式によって決まる:
はStefan-Boltzmann定数である。このガス温度は状態方程式によって決まる:
(10)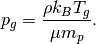
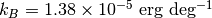 はボルツマン定数、
はボルツマン定数、 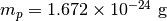 はイオン質量、
はイオン質量、 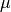 は平均分子量である。
は平均分子量である。
これらの式に加えて、クロージャー関係と呼ばれる 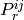 を与える式(輻射の状態方程式)が必要となる。ここでは2つのクロージャー関係式を紹介する。
を与える式(輻射の状態方程式)が必要となる。ここでは2つのクロージャー関係式を紹介する。
共動座標系で等方的な放射を仮定した場合、 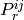 は
は
(11)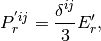
と表される。このように等方的な輻射圧を与える近似を Eddington近似 と呼ぶ。ダッシュ  は共動座標系の物理量を表しているが、式 (4) - (8) で必要なのは観測者系のストレス
は共動座標系の物理量を表しているが、式 (4) - (8) で必要なのは観測者系のストレス 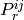 である。そこで式 (11) にローレンツ変換を用いることで
である。そこで式 (11) にローレンツ変換を用いることで 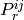 に対する関係式が得られる:
に対する関係式が得られる:
(12)![P^{ij}_r
&+ \left[ -\frac{\delta^{ij}}{3}\frac{u_k u_l }{c^2}
+\frac{u^i u^j u_k u_l}{(1+\gamma)^2 c^4} \right] P_r^{kl}
+\frac{u^i u_k P_r^{jk} + u^j u_k P_r^{ik}}{(\gamma+1)c^2}
\\
&= \frac{\delta^{ij}}{3}\gamma^2
\left(E_r - 2 \frac{\beta_j F_r^j}{c}\right)
-\frac{u^i u^j E_r}{c^2}
+\frac{u^i F_r^j + u^j F^i_r}{c^2}
+\frac{2 u^i u^j u_k F_r^k}{(\gamma+1)c^4}.](_images/math/67db287f39b1ee9c02428108ee7d388115e34dcd.png)
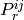 は
は 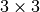 の対称行列のため、
の対称行列のため、 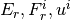 を与えて
を与えて 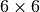 の線形方程式を解くことで
の線形方程式を解くことで 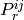 が得られる。
が得られる。
Eddiington近似は光学的に厚い状況では正しいが、光学的に薄い場合放射は等方的にならないため正しくない。非等方な放射を考慮したクロージャーとして M-1クロージャー が提案されている:
(13)![P_r^{ij} = \left[\frac{3(1 - \chi)}{2}\frac{\delta^{ij}}{3}
+ \frac{3\chi - 1}{2}n^i n^j\right]E_r](_images/math/07add7cb278644c5fda6e910aa4c9216a2b1c314.png)
(14)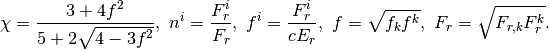
課題¶
熱平衡状態への遷移 “1d_lte/”¶
ガス温度と輻射温度( 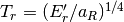 、ただし
、ただし 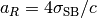 )が等しくない場合、ガスと輻射は吸収・再放射を通してエネルギーのやり取りを行い、熱平衡状態(
)が等しくない場合、ガスと輻射は吸収・再放射を通してエネルギーのやり取りを行い、熱平衡状態( 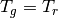 )へと近づいていく。この節では非熱平衡状態から熱平衡状態へと遷移していく過程を考える。
)へと近づいていく。この節では非熱平衡状態から熱平衡状態へと遷移していく過程を考える。
仮定としてガスは定常・静的とし、ガス密度( 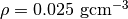 )、ガス温度(
)、ガス温度( 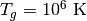 )は一定とする。吸収係数は
)は一定とする。吸収係数は 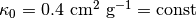 とし、散乱係数は
とし、散乱係数は 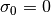 とする。輻射温度は初期に
とする。輻射温度は初期に 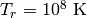 とする。
とする。
- 吸収を通して輻射エネルギーが減少し、熱平衡状態に近づいて行くことを確認してください。特に$t-log E_r$でプロットした場合、どのように輻射エネルギーが減衰するかを確認してください。
- 輻射エネルギーが指数関数的に減衰する理由を考えてみてください。(ヒント: 式 (4) で
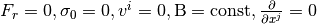 とする。)
とする。)
1次元輻射の伝搬 “1d_transport/”¶
輻射場がガス中を伝搬すると、輻射場は吸収過程により減衰しながら伝搬していく。この節では1次元一様静的なガス中を伝搬する輻射場を考える。
計算領域のサイズは 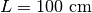 で、ガス密度、ガス温度はそれぞれ
で、ガス密度、ガス温度はそれぞれ 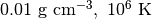 とし、輻射場はガスと熱平衡にあるとする。吸収係数は
とし、輻射場はガスと熱平衡にあるとする。吸収係数は 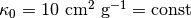 とし、散乱係数は
とし、散乱係数は 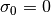 とする。この一様媒質中に
とする。この一様媒質中に 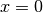 から輻射を
から輻射を 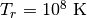 で照射する。
で照射する。
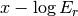 上で輻射が時間とともに伝播していく様子を確認してください。
上で輻射が時間とともに伝播していく様子を確認してください。- 吸収係数を変更した場合( initial.f90 内の変数 absorption )、どのように変化するか確認してください(ただし大きすぎると数値的に解けなくなります)。
- クロージャー関係を変えた場合( initial.f90 内の変数 radiation を1から2に変更)、波面の伝播する速度が変わることを確かめ、なぜそのようになるか考えてください(ヒント: 光学的に薄い極限を考え、式 (4) - (5) で
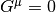 とし、Eddington近似の場合は
とし、Eddington近似の場合は 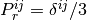 、M-1クロージャーの場合は
、M-1クロージャーの場合は 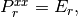 その他
その他 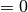 として特性速度を求めてください)。
として特性速度を求めてください)。 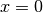 から注入された光の波面が
から注入された光の波面が 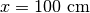 の境界を通過すると定常状態になるの定常状態になったときの、
の境界を通過すると定常状態になるの定常状態になったときの、 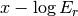 の傾きをEddington近似を用いた場合とM-1クロージャーを用いた場合でそれぞれ求めてください。また、その傾きが何によって決まるかを考えてみてください。(ヒント: 式 (4) (5) で定常・静的なガスを仮定し、
の傾きをEddington近似を用いた場合とM-1クロージャーを用いた場合でそれぞれ求めてください。また、その傾きが何によって決まるかを考えてみてください。(ヒント: 式 (4) (5) で定常・静的なガスを仮定し、 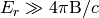 とする。)
とする。)
2次元輻射場の伝播 〜日陰問題〜 “2d_shadow/”¶
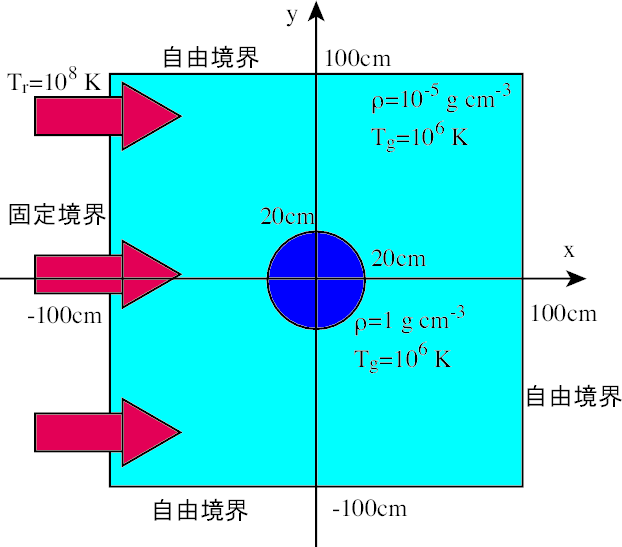
2次元輻射場伝播問題の初期条件。
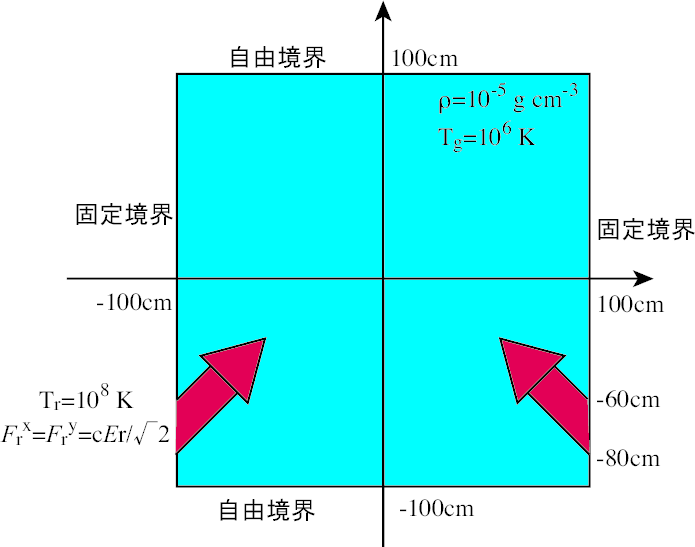
輻射衝突の計算。
この節では光学的に厚い物体に光を照らした場合の計算を行う( 2次元輻射場伝播問題の初期条件図 )。密度 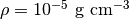 、温度
、温度 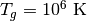 の熱平衡にある一様媒質中に半径
の熱平衡にある一様媒質中に半径 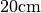 の重たいクランプ
の重たいクランプ 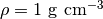 を置く。このクランプに対して
を置く。このクランプに対して 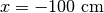 の境界から温度 :math`T_r = 10^8mathrm{K}` の輻射を照射する。吸収係数は
の境界から温度 :math`T_r = 10^8mathrm{K}` の輻射を照射する。吸収係数は 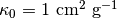 、散乱係数は
、散乱係数は 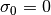 とする。
とする。
- Eddington近似を用いた場合とM-1クロージャーを用いた場合でどのように結果が変わるか確認してください。
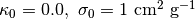 とした場合( initial.f90 内 absorption = 0, scattering=1 )、どのように結果が変わるか確認してください。
とした場合( initial.f90 内 absorption = 0, scattering=1 )、どのように結果が変わるか確認してください。
2次元輻射場の伝播 〜輻射の衝突〜 “2d_collision/”¶
光学的に薄いガス中を伝播する2本の光柱を考える( 輻射衝突の計算の設定図 )。ガスは一様静的とし、密度 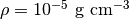 、温度
、温度 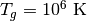 とする。以下の様に境界から光を注入し、二つの光が交差する様子を確かめる。
とする。以下の様に境界から光を注入し、二つの光が交差する様子を確かめる。
(15)![E_r = a_R T_r^4,\ F_r^x = F_r^y = \frac{c E_r}{\sqrt{2}}, & \ if\ x \le
-100\ \mathrm{cm}\ and \ y = [-80\ \mathrm{cm}, -60 \ \mathrm{cm}],\\
E_r = a_R T_r^4,\ -F_r^x = F_r^y = \frac{c E_r}{\sqrt{2}}, & \ if\ x \ge
100\ \mathrm{cm}\ and \ y = [-80\ \mathrm{cm}, -60 \ \mathrm{cm}],\\](_images/math/08b3d98c6449359d29297b929e78fa6bf84959c0.png)
ただし 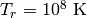 とする。吸収係数、散乱係数はともに
とする。吸収係数、散乱係数はともに 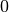 とし、M-1クロージャーを用いる。
とし、M-1クロージャーを用いる。
- 2本の光柱が真っ直ぐに進み、衝突することを確認してください。
- 光同士は相互作用をしないため、光が衝突することは非物理的である。なぜこのような事が起きるのか考えてみてください。
- 2本の光の強度が異なる場合にどうなるか調べてみてください。
(発展編)2次元輻射場の伝播 〜ガスの加速〜 2d_acc/¶
ここでは輻射によってガスが加速されて行く様子を計算する。計算ボックスは2次元 ![x=[-10^{4}, 3\times 10^4]\ \mathrm{cm}](_images/math/349c2396aa28a025fff1d392658d7be068143a0a.png) 、
、 ![x=[-2\times 10^{4},2\times 10^4]\ \mathrm{cm}](_images/math/8d9c1a0ecd4ff3dcc2fb5a933cd5c04dc6cceaf4.png) とし、一様なガス(
とし、一様なガス( 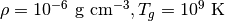 )で満たす。ここに円筒形のガスクランプ(半径
)で満たす。ここに円筒形のガスクランプ(半径 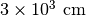 、密度
、密度 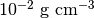 )をおき、
)をおき、 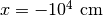 から輻射を照射する(
から輻射を照射する( 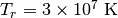 )。この問題ではガスの運動を追うため、静的なガスを仮定しない ( initial.f90 内、変数 hydro = .true. )。ガスクランプが加速されていく様子を確かめてください。
)。この問題ではガスの運動を追うため、静的なガスを仮定しない ( initial.f90 内、変数 hydro = .true. )。ガスクランプが加速されていく様子を確かめてください。