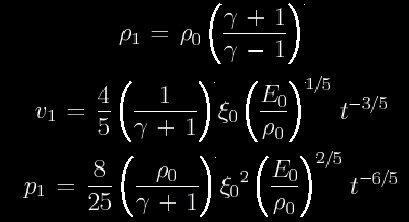

The exact solution of point explosion is called as Sedov-Taylor self similar
solution and well known as a basic model on the evolution of supernova
explosion.
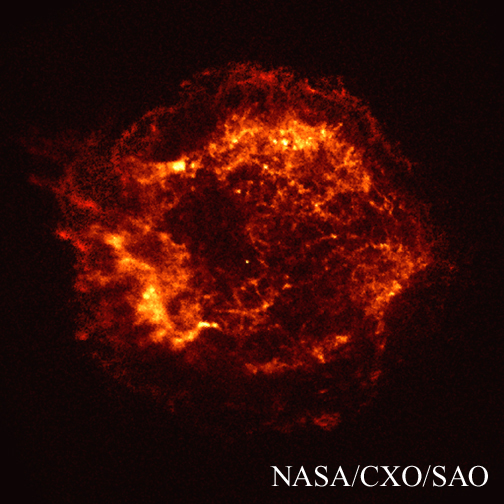
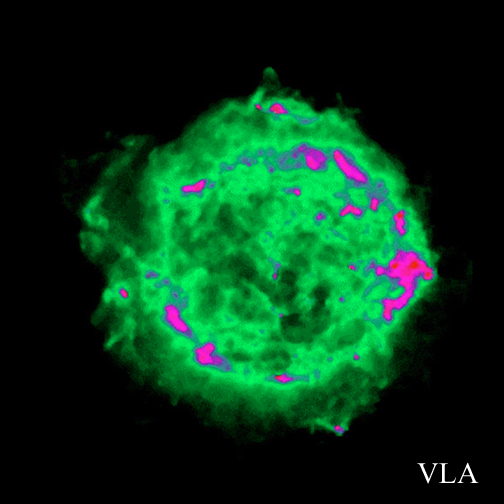

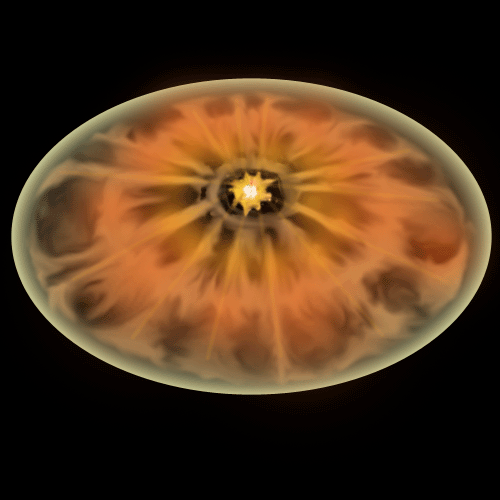
Above figures are the photographs of the typical supernova remnant CasA in
X-ray, non-thermal radio, and optical radiations from left to right,
respectively. This 'cloud' has about 10 light years diameter and is regarded
as a figure of spherical shock wave generated by the supernova explosion
took place about 300 years ago and being expanded into the inter stellar
medium.
From the observed X-ray spectrum, the gas emitted this X-ray has temperature
as high as 50 million K. From its intensity distribution, high temperature
gas is considered to distribute spherically. The outer most surface is the
shock wave
front and the scene where the shock wave heats up the inter stellar gas
entrained by the expanding shock wave is seen.
On the otherhand, the strong polarized non-thermal radio emission is observed
in radio (VLA) observation, this is the result of synchrotron emission
emitted from relativistic electrons circulating around magnetic filed lines.
It is considered that electrons are accelerated up to very high energy by
Fermi acceleration at the shock surface.

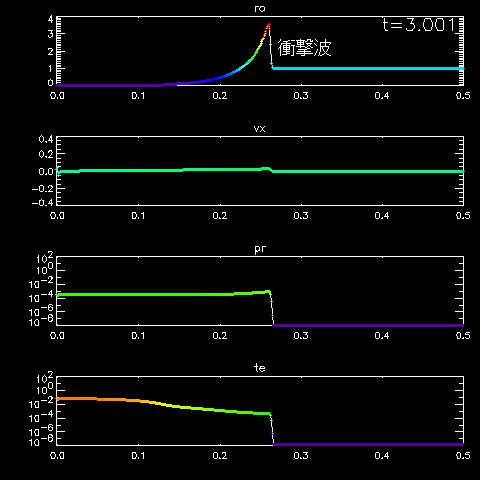
To show initial states, please place the mouse on the figures.
High temperature and high pressure gas at the center is expanding along with
swept up surrounding low temperature gas (adiabatic expansion).
Please refer detailed explanation for the simulation results in detail.

Spherically symmetric Hydrodynamic equations.


Free Expansion Phase
Initially, envelope ejected by the supernova explosion is expanding freely
into the interstellar medium. Then this expanding envelope compresses
interstellar gas around it, creates a shock wave inside of the interstellar
gas because of high expanding velosity, and sweep up the inter stellar gas
along with its expansion. During this initial phase, the amount of gas swept
up is much smaller than the original exploded envelope, the expantion of the
envelope is not affected by the outer interstellar gas and kept initial
speed and energy.
Adiabatic Expansion Phase
When the amount of gas swept up becomes larger than the original exploded
envelope, Kinetic energy of the original exploded envelope is transfered to
the swept up gas, the shock wave is propagating into interstellar gas, and
the swept up gas is heated up by the shock wave despite of the details of
explosion. The period during when energy is not released by the radiation
from the swept up gas (when energy is conserved) is called adiabatic expansion
phase. The evolution during this phase is determined only by the energy of
explosion E0, the density of interstellar gas
![[roh]](../elogo/roh0.gif) , and the
elapsed time from the explosion t.
Then a self similar solution exists as shown in the next section,
the thermodynamic quantities of hot gas inside the shock front, e.g., density,
pressure, and temperature of the gas, and the distribution of the expansion
velocity is well described by the Sedov-Taylor self similar solution. The
way to derive Sedov-Taylor self similar solution is found in "Fluid
Mechanics" by Landau and Lifshitz, "Similarity Methods in Mechanics" by L. I.
Sedov, and/ or "Uchu Ryutai Rikigaku (in Japanese)" by Sakashita and Ikeuchi.
, and the
elapsed time from the explosion t.
Then a self similar solution exists as shown in the next section,
the thermodynamic quantities of hot gas inside the shock front, e.g., density,
pressure, and temperature of the gas, and the distribution of the expansion
velocity is well described by the Sedov-Taylor self similar solution. The
way to derive Sedov-Taylor self similar solution is found in "Fluid
Mechanics" by Landau and Lifshitz, "Similarity Methods in Mechanics" by L. I.
Sedov, and/ or "Uchu Ryutai Rikigaku (in Japanese)" by Sakashita and Ikeuchi.
Constant Temperature Expanding Phase
The expansion velocity is decreasing with time. As a result, when the
expansion proceeds, radiation cooling behind the shock front becomes
effective. Because the energy loss per unit volume and unit time by radiation
cooling (radiation cooling rate) becomes larger along with the decrease in
temperature (decceleration of shock wave). When radiation cooling time of the
gas becomes shorter than the expansion time, the evolution deviates from
self similar one. Then radiation cooled interstellar gas distributes
spherically (shperical shell) behind the shock wave, hot rarefied gas fills
inside it. This phase of supernova remnant (SNR) is called in constant
temperature expanding phase. In this phase, the SNR evolves under rather
conserving momentum of the cooled down high density shell (spherical shell)
of inter stellar gas than conserving energy. In this phase, the radius
of the shell expands in proportion to 1/4 power of the elapsed time
since the explosion.
Brief Explanation on Sedov-Taylor Solution
As an initial condition, energy E0 is released at the center
of isotropic gas with constant density
![[roh]](../elogo/roh0.gif) .
It is too much complicated to describe exeact solution completely,
we will write down characteristic physical quantities of the exact solution
here.
Time evolution of the radius R and expanding velocity D of the shock front
are described as
.
It is too much complicated to describe exeact solution completely,
we will write down characteristic physical quantities of the exact solution
here.
Time evolution of the radius R and expanding velocity D of the shock front
are described as
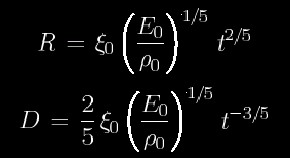 Here,
Here, ![[Xi]](../elogo/xi0.gif) is a
dimensionless constant determined by specific heat ratio
is a
dimensionless constant determined by specific heat ratio
![[gamma]](../elogo/gamma.gif) . Typical values are
listed in the Table below.
. Typical values are
listed in the Table below.
 At just behind the shock wave (r=R), time evolution of physical quantities
are described as follows.
At just behind the shock wave (r=R), time evolution of physical quantities
are described as follows.
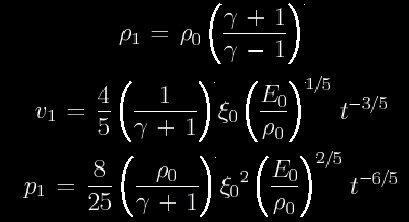 Please refer THIS document (PDF file in Japanese)
for detailed explanation.
Please refer THIS document (PDF file in Japanese)
for detailed explanation.

"Fluid Mechanics (Course of Theoretical Physics, Vol. 6)", Landau and
Lifshitz, 1959, Read Edu. & Prof. Publ. Ltd.
"Similarity and Dimensional Methods in Mechanics", L. I. Sedov, 1982,
Mir Publ., Moscow.
"Uchu Ryutai Rikigaku (in Japanese)", Sakashita and Ikeuchi, Baifukan.










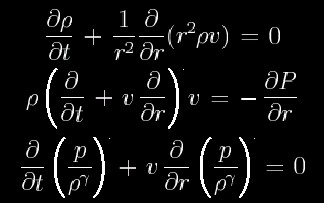


![[roh]](../elogo/roh0.gif) , and the
elapsed time from the explosion t.
Then a self similar solution exists as shown in the next section,
the thermodynamic quantities of hot gas inside the shock front, e.g., density,
pressure, and temperature of the gas, and the distribution of the expansion
velocity is well described by the Sedov-Taylor self similar solution. The
way to derive Sedov-Taylor self similar solution is found in "Fluid
Mechanics" by Landau and Lifshitz, "Similarity Methods in Mechanics" by L. I.
Sedov, and/ or "Uchu Ryutai Rikigaku (in Japanese)" by Sakashita and Ikeuchi.
, and the
elapsed time from the explosion t.
Then a self similar solution exists as shown in the next section,
the thermodynamic quantities of hot gas inside the shock front, e.g., density,
pressure, and temperature of the gas, and the distribution of the expansion
velocity is well described by the Sedov-Taylor self similar solution. The
way to derive Sedov-Taylor self similar solution is found in "Fluid
Mechanics" by Landau and Lifshitz, "Similarity Methods in Mechanics" by L. I.
Sedov, and/ or "Uchu Ryutai Rikigaku (in Japanese)" by Sakashita and Ikeuchi.
![[roh]](../elogo/roh0.gif) .
It is too much complicated to describe exeact solution completely,
we will write down characteristic physical quantities of the exact solution
here.
Time evolution of the radius R and expanding velocity D of the shock front
are described as
.
It is too much complicated to describe exeact solution completely,
we will write down characteristic physical quantities of the exact solution
here.
Time evolution of the radius R and expanding velocity D of the shock front
are described as
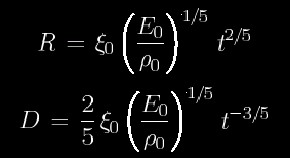
![[Xi]](../elogo/xi0.gif) is a
dimensionless constant determined by specific heat ratio
is a
dimensionless constant determined by specific heat ratio
![[gamma]](../elogo/gamma.gif) . Typical values are
listed in the Table below.
. Typical values are
listed in the Table below.