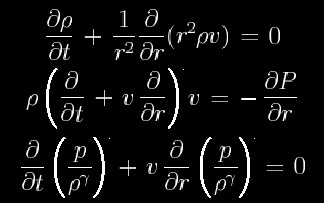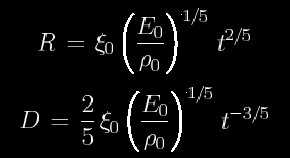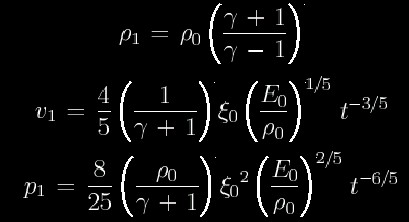
点源爆発の厳密解はセドフテイラー自己相似解とよばれ、超新星爆発の進化の
基礎モデルとして知られています。
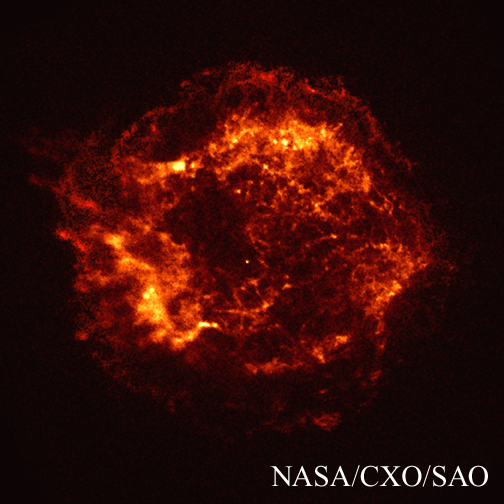
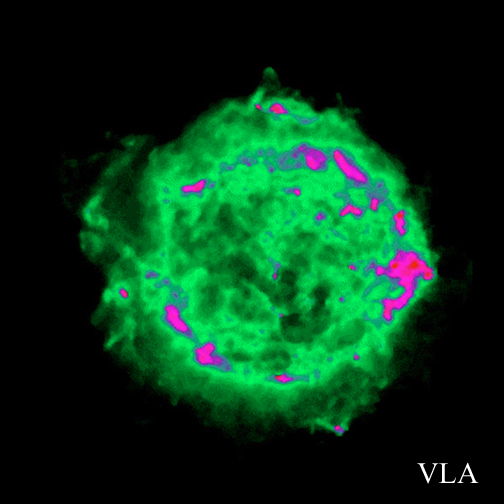
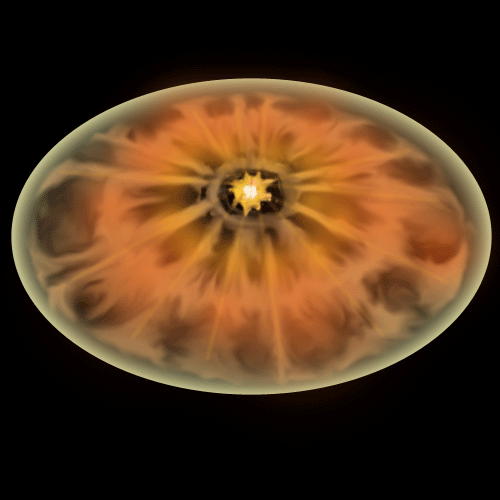
画像は典型的な超新星残骸であるCas Aの左からX線、非熱的電波、可視光による写真
です。この「星雲」は差し渡しおよそ１０光年で、ほぼ300年前に爆発した超新星に
よって生じた球状の衝撃波が星間空間に広がっている姿を見ているものと考えられて
います。
観測されるX線のスペクトルからこれを放出しているガスの温度が5千万度に達している
ことがわかります。
その強度分布から、高温ガスは球状に分布していると考えられます。
最も外側の部分が衝撃波面で、衝撃波が星間空間を広がりながら取り込んだ星間物質を
加熱して行っている様子をみていることになります。
また電波観測で（VLA）は偏光した非熱的電波が強く見られますが、これは、
相対論的な電子が磁力線の回りを回転するときに出すシンクロトロン光です。
衝撃波面で電子がフェルミ加速によって高いエネルギーまで加速されていると
考えられています。
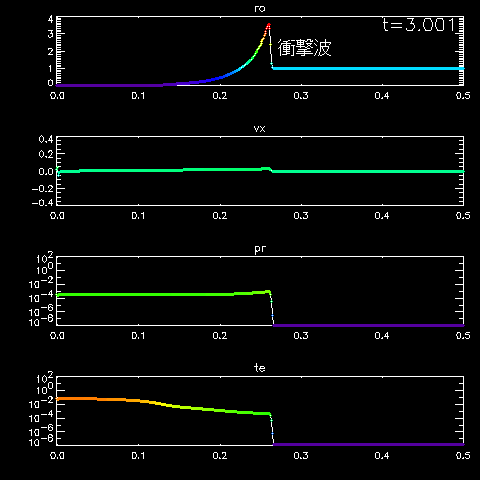
初期条件を表示するにはマウスを図の上においてください。
中心にあった高温・高圧のガスは
周りの低温のガスをかき集めながら膨張していきます(断熱膨張期)。
計算結果について詳しくは詳細解説をごらんください。
球対称の流体方程式
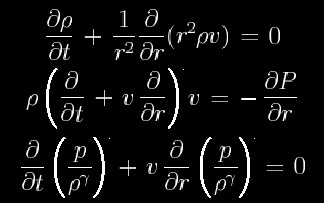
自由膨張期
初期には爆発で放出された星の外層がほぼ自由に星間空間を膨張します。
それは星の外層は周りに存在した星間気体を圧縮し、高速の膨張のために
星間物質中に衝撃波を生じ、星間気体をかき集めながら膨張してゆきます。
初期にはかき集められる量は外層の質量に比べて非常に少ないので、
星の外層の膨張は外の星間気体には影響されずに初期の速度、運動エネルギーを
保って膨張します。
断熱膨張期
しかし、かき集められた外の星間気体の質量が爆発した星の外層のそれを
上回るようになると、星の外層の持っていた運動エネルギーは、かき集められた
星間気体に渡され、はじめの爆発の詳細によらず、衝撃波が星間気体の中へ膨張し、
取り込まれたガスは過熱されるという状態に移行します。
このとき、取り込まれた星間ガスからの輻射冷却によってエネルギーが失われない
（エネルギーが保存している）段階は断熱膨張期と呼ばれます。
このときの進化は爆発のエネルギーE0、
周りの星間物質の密度ρ0と、爆発後の時間ｔのみで
決まっていることが知られています。
このときは次の章で見るように自己相似的な解が存在し、衝撃波の内側の高温気体の
密度、圧力、温度などの熱力学的量や膨張速度の半径分布はセドフｰテイラー
自己相似解でよくあらわされることが知られています。
セドフｰテイラー自己相似解の求め方についてはランダウ・リフシッツ「流体力学」、
坂下・池内「宇宙流体力学」を参照してください。
等温膨張期
衝撃波の速度は時間とともに減少します。その結果、さらに膨張が進むと、
衝撃波の後面で輻射冷却が効き始めます。
それは単位時間当たり単位体積あたりの輻射冷却によって失われるエネルギー
（輻射冷却率）が温度の減少（衝撃波の減速）とともに大きくなるようになるから
です。輻射冷却によってガスが冷却する時間が膨張する時間に比べて短くなると、
もはや、断熱の仮定は成り立たなくなり、自己相似的な進化から外れてきます。
このときは、衝撃波の後ろには輻射冷却によって冷えた星間気体がシェル
（球殻）状に分布し、その内側にはなお高温な希薄な気体が満ちている構造を
とるようになります。このような時期の超新星残骸を等温膨張期と呼びます。
もはやエネルギー保存はなりたたず、むしろ、シェル（球殻）状の冷えて密度の
高まった星間気体の運動量が保存するように膨張が進みます。
このときはシェルの半径は爆発後の時間の1/4乗に比例して膨張することが
知られています。
セドフ・テイラー解の簡単な説明
初期状態としては、エネルギーE0をもつ点源爆発と
点源爆発を覆っている密度ρ0の気体を考えています。
厳密解をすべて記述することは複雑ですので、
ここでは厳密解の特徴をあらわす物理量について式をあらわします。
衝撃波面の半径Rと衝撃波の膨張速度Dは
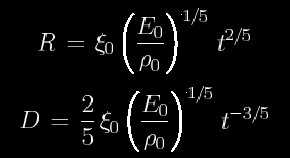といった時間進化をとります。
ここで、ξ0は気体定数γによって定まる無次元量の定数です。
代表的な値を以下の表の通りです。
衝撃波の後(r=R)での物理量は
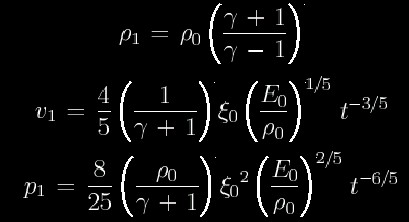といった時間進化をとります。
より詳しくは、こちらのドキュメント(PDFファイル)を参照してください。
坂下志郎、池内了共著、宇宙流体力学、培風館