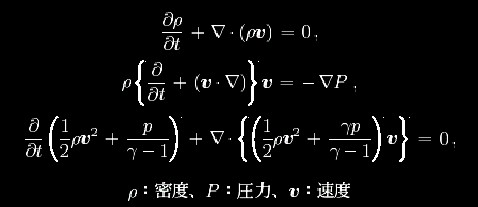
Shock tube problem is a problem to follow the evolution of fluids with same
specific heat but different thermodynamic states placed in the tube with
constant cross section after removing the divided partition.
Because its solution has typical physical phenomena such as a shock wave,
contact discontinuity, and rarefaction wave, and it also has exact solution,
the shock wave problem is used for the fundamental check of the simulation
code. It is basically 1 dinemsional problem but, for 2 and/or 3 dimensional
code, partition is placed on the skew and it used as a check for the transmit
of physical quantities to the oblique direction.
To show initial states, please place the mouse on figures.
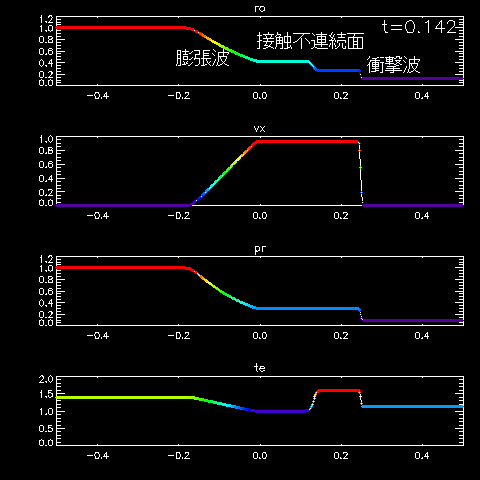
Three characteristic waves are transmitted.
From leftside, smooth curve between corners is Expanding wave,
density discontinuity with constant pressure is Contact Discontinuity,
discontinuity in all physical quantities at the right hand side is Shock wave.
Please refer detailed explanation for detailed numerical results.
Hydridynamic Equations
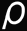is density, P is pressure,
and v is velocity.
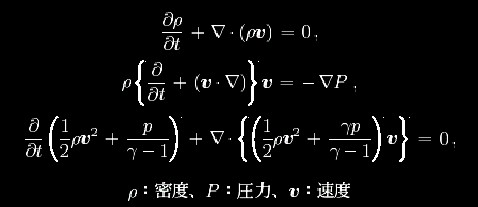
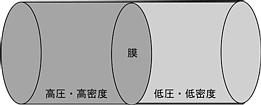
Fluid states after removing the partition have different characters in
- region in front (right side) of the shock,
- region between the contact discontinuity and the shock,
- region between the expansion wave and the contact discontinuity,
- region of the expansion wave,
- region behind (left side) of the expansion wave.
Please refer THIS document (PDF file in Japanese)
for detailed explanation.