Appendix¶
共役勾配法(Conjugate Gradient method)¶
- 著者:
簑島敬(JAMSTEC)
共役勾配法(Conjugate Gradient method, CG法)とは、 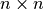 対称正定値行列
対称正定値行列 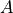 を係数とする
を係数とする 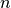 元連立一次方程式
元連立一次方程式
(1)¶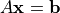
を解くためのアルゴリズムです。
式 (1) の解を、 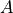 に関して互いに共役 [1] なベクトル
に関して互いに共役 [1] なベクトル 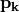 を用いて
を用いて
(2)¶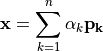
と展開し、 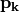 と係数
と係数 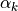 を逐次求めていくことで、解を探索します。
を逐次求めていくことで、解を探索します。
ある関数 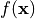 を2次までのテイラー展開で近似します。
を2次までのテイラー展開で近似します。
(3)¶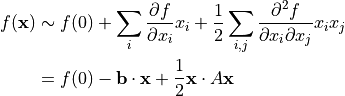
式 (3) の近似では、 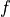 の勾配は
の勾配は
(4)¶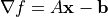
となり、式 (1) の解を求めることは、 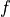 の極値(最小値)を求めることに相当します。
の極値(最小値)を求めることに相当します。
ある方向 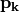 に沿って
に沿って 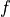 を最小化し、次に新しい方向
を最小化し、次に新しい方向 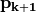 に沿って
に沿って 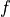 を最小化する際に、
を最小化する際に、 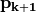 を過去全ての
を過去全ての 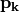 と
と 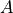 に関して共役に選ぶと、新しい最小化の方向と過去の最小化による勾配の変化の方向との関係は
に関して共役に選ぶと、新しい最小化の方向と過去の最小化による勾配の変化の方向との関係は
(5)¶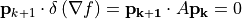
と垂直になるので、新しい最小化は過去の最小化に干渉しません。こうすることで、 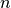 次の行列に対して高々
次の行列に対して高々 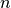 回の計算で解を探索することが出来ます。
回の計算で解を探索することが出来ます。
具体的なアルゴリズムは以下のようになります。
初期化。
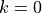 ,
, 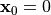 , 残差
, 残差 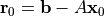 ,
, 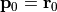
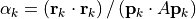
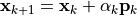
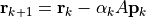
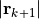 が十分小さければ、
が十分小さければ、 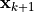 は真の解に収束したとみなして、計算終了。
は真の解に収束したとみなして、計算終了。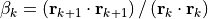
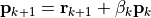
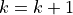
1に戻る。
Footnotes
