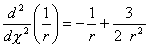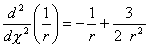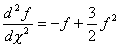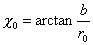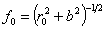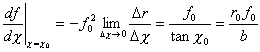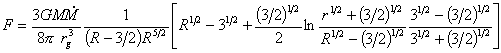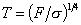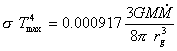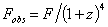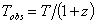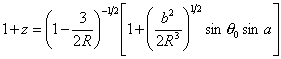study
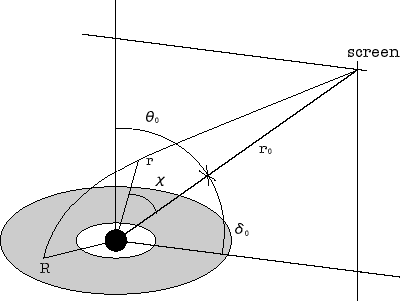
	私は卒業研究として、一般相対論的光線追跡法による ブラックホール近傍の降着円盤像の作成を行った。 光線追跡法については、１９８７年に書かれた福江純さんの論文を参考にした。 下に簡単な図を示す。
	黒い球がブラックホール、その周りの円盤が降着円盤である。 円盤から出た光をスクリーンで受ける。 軌跡は、福江（1987年）の（1）式から下の式に従う。
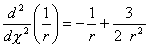
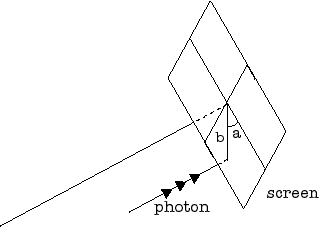
	式中のｒは、ブラックホールの中心から光子までの距離で、 χは図に示すような角度である。 ｒの単位はシュバルツシルト半径を単位としている。 光子の軌跡にはもうひとつ条件があり、 それは軌跡がＲとｒoの直線を含む平面内にあるということである。 図の内側の楕円は降着円盤の内側の半径をあらわしている。 ここはブラックホールの半径の３倍となっている。 ここより内側には降着円盤は存在しない。 実際に光は円盤からスクリーンへという経路をたどるが、 計算はスクリーン上の光の到達点から始めて、 円盤上の光の発射点まで行う。 次にスクリーンについて説明する。 スクリーンは下図のように光子を受ける。
	スクリーンは、垂直に入射する光のみを写すものとする。 スクリーンのサイズは30rg×30rgである。 rgはブラックホールの半径である。 スクリーンには入射光に相当する温度をプロットする。 スクリーンの位置はブラックホールの中心から10000rgの距離にあるとする。 また、円盤のある平面からの角度δoが5°、10°、20°、30°の４種類とする。 実際に計算するときはスクリーンを縦横２０１×２０１に分割して、 そのマス目ごとに光線追跡法を用いて、円盤上の光の発射点を求める。 被写体となる降着円盤について説明する。 質量Mのシュバルツシルトブラックホール周辺の 幾何学的に薄い降着円盤である。 降着円盤の内側の半径は、中心のブラックホールの半径 （シュバルツシルト半径）の3倍である。 降着円盤は撮影者から見て、その視線方向に対して 半時計回りに回転しているとする。 それでは、実際に光線を追跡する。 ここではルンゲクッタ法を用いて光線を追跡する。 軌跡をあらわす式は
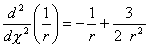
	である。 計算はスクリーン上の光の到達点から始めて、 降着円盤上の光の発射点まで行う。 簡単のためにf=1/rとする。 すると
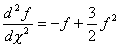
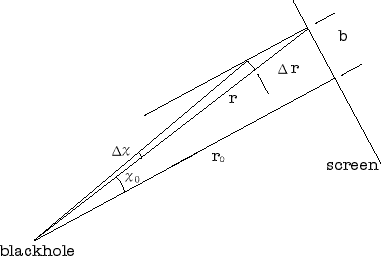
	である。 それでは、計算の初期条件と終了条件を説明する。 計算の始点はスクリーン上の光の到達点なので、 その位置によって初期条件が決まる。 実際の初期条件は図のχoと、 ブラックホール中心からスクリーン上の点までの距離ｒの逆数ｆoである。
	図を見ると分かるようにχoは
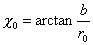
	である。またfoは
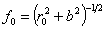
	である。もうひとつの初期条件はｆの一階微分であるが、これも図の求めて、
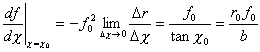
	となった。次に終了条件についてだが、 計算の終点は円盤上である。 円盤上に達した時点で計算を終了する。 実際の終了条件は少々複雑なので省略するが、、 １９７９年のルミネの論文の（９）式から求めることができる。 光線追跡法によって求めた円盤上の光の発射点の半径Ｒから、 その点の輻射流束Ｆと温度Ｔを求めることができる。 Ｆ，Ｔはそれぞれ
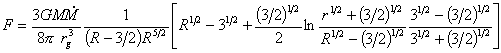
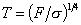
	である。 計算ではＭとアクリーションレイトの代りに円盤状の最高温度Tmaxを使う。 Tmaxの式はＦの式を微分することによって得られる。 今回の計算ではTmaxを10000000Kとする。 これは恒星サイズのブラックホール周辺の円盤の温度程度である。
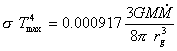
	次に円盤の回転によるドップラー効果と、 ブラックホールによる重力赤方偏移の効果を考える。 実際に観測される輻射流束や温度は、 上のＦ，Ｔとは違うものになる。 それは円盤が回転している影響と、重力による赤方偏移の影響のためである。 赤方偏移をｚとすると観測される輻射流束、温度は
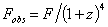
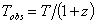
	のようになる。 ｚはルミネ（1979年）の（19）式から決定される。
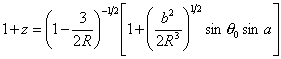
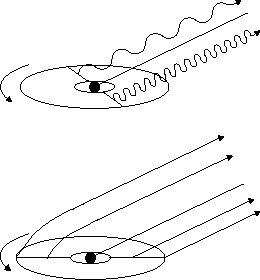
	それでは、実際にスクリーンにプロットされる温度分布を示す。 写真はδoが5°、10°、20°、30°の4種類である。 5°の写真 10°の写真 20°の写真 30°の写真 色の配色は高い方から黄色、オレンジ、緑、青、黒となっている。 黄色の部分は温度が12000000K以上のところである。 中心付近の黒は降着円盤が存在しない、半径３rg以下の部分を示している。 外側の黒い部分は降着円盤は存在しているところで、 温度が3000000K以下の部分を示している。 角度が小さいほど温度分布が横に細長くなっているのは、 円盤のある面に対して低い角度から見ているためである。 温度分布が上下左右非対称となっているのは 赤方偏移の効果と重力レンズの効果のためである。 最後に今回の研究のまとめをする。 スクリーン上の温度分布が左右非対称になっていることについて、 簡単にまとめたいと思う。 まず左右の非対称性だが、、これは図に示すように、 回転により、左右の波長の長さが変わっていることが 原因であると考えられる。 当然波長の短い方が温度が高いということになる。 一方、上下の非対称性については、図に示すように、 重力レンズにより下の方に比べて上の光線が浮いているようになっているのが原因である。
	一応、最後にプログラムを示す。 言語はｃである。 動く保証はなし。 プログラム
	以上、終わり。
	トップページに戻る