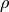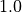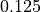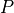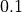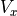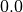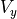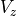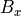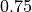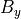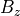衝撃波管問題¶
- 著者
松本洋介（千葉大学）
背景¶
MHDシミュレーションコードをテストする標準問題として、衝撃波管問題が知られている。これは、シミュレーションの系（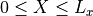 
）の左側（ 
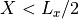）と右側（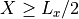 
）を異なる状態で初期に設定し、その後の系の発展を見るものである。これはちょうど、近似リーマン解を求める際のセル境界における左・右状態を設定するのと同じである（ 近似リーマン解法参照 ）。結果として現れる、接触不連続、接線不連続、回転不連続、速・遅衝撃波、膨張波などが正しい速度で伝搬するか、を検証することができる。また、不連続近傍における数値振動、解像度（何セルで表現できるか）を計算スキームによって比較するためにもしばしば採用される。本課題では、 Brio & Wu (1988) の衝撃波管問題を例に取って、計算結果例を紹介する。
課題設定¶
以下にシミュレーションの初期設定をまとめる。設定は''model.f90''で行っている。なお、オリジナルの設定と違い、比熱比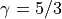 
である（ Ryu & Jones, 1995 参照）。
物理量
左状態（
右状態（
結果¶
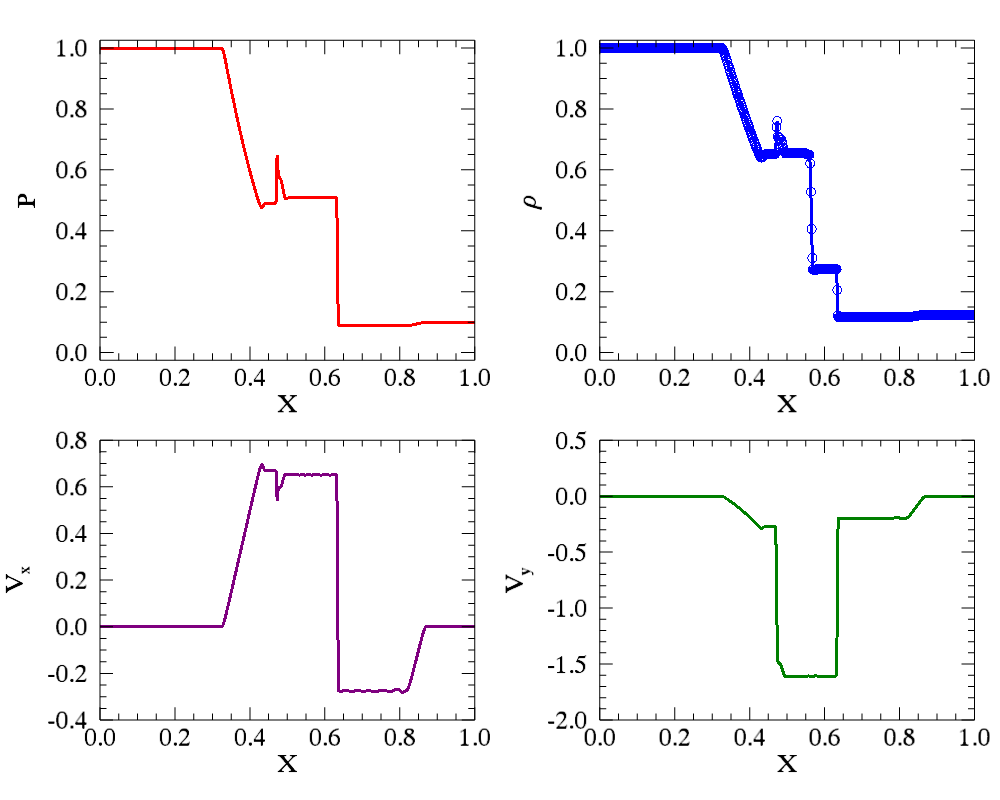
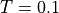における結果。左上→右上→左下→右下の順に、圧力、質量密度、速度ｘ成分、速度ｙ成分を表す。¶
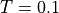における結果を 図 に示す。右上の質量密度から、左から順に、速い膨張波、slow compound波（ 
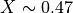）、接触不連続（ 
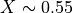）、遅衝撃波（ 
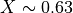）、速い膨張波が形成される。これら不連続周辺で若干の数値振動が残るものの、 CANS+ の特徴である高次精度化により、数点で解像できていることがわかる。
まとめ¶
本課題では Brio & Wu (1988) を例にとったが、様々な設定例が Ryu & Jones (1995) に掲載されているので、参考にしてテストを行ってみるとよい。