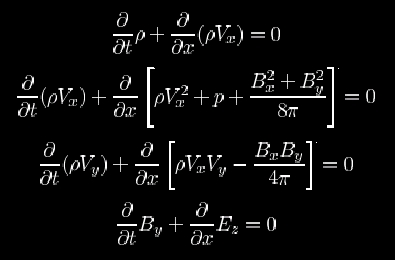

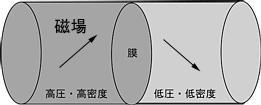
MHD Shock Tube problem is an application of Hydrodynamic shock tube problem
to the Magneto Hydrodynamics and the fundamental check problem for MHD
simulation codes. As like the Hydrodynamic shock tube problem, fluids which
have different thermal conditions or magnetic field
are placed at the both sides of the tube which has constant cross
section and simulate their evolution.

To show initial states, please place the mouse on figures.
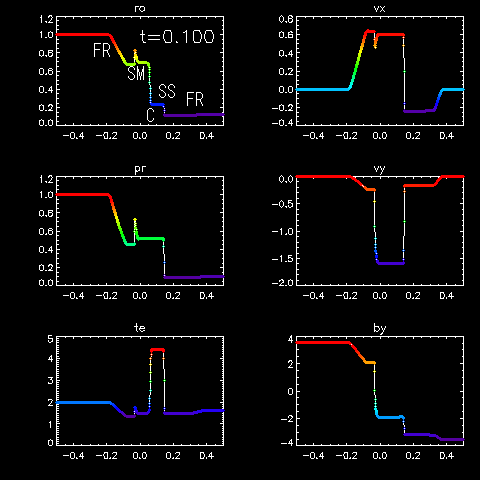
Five typical waves are transmitted.
From leftside, smooth curve between corners is Fast expanding wave (FR),
steep peak is Slow compaound wave (SM), density discontinuity with constant
pressure is Contact discontinuity (C), discontinuity in all physical
quantities is Shock wave (SS), and smooth curve between corners at the right
hand side is Fast expanding wave (FR).
Please refer detailed explanation for detailed numerical results.

Magneto Hydrodynamic equations
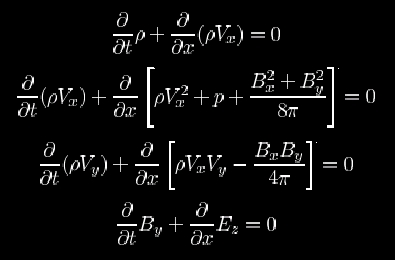
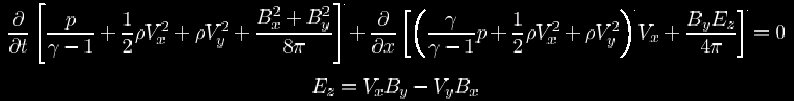

MHD shock tube problem has been proposed by Brio & Wu (1988) and Ryu & Jones
(1995). Here, we will apply the initial conditions proposed by Brio & Wu
(1988), and follow the evolution. As the initial model, in addition to the
discontinuities in density and pressure, curved magnetic fields threading
fluids is the attribute of their model.
Characteristics on the time evolution of their model are as follows.
- Fast expanding (rarefaction) wave is formed to the high temperature
and high density side of the initial discontinuity of the gas fluid.
- Contact discontinuity in density is formed.
- Slow compound wave is formed behind the contact discontinuity.
Compound wave is a characteristic wave which appeared in MHD shock tube
problem. It is a rarefaction wave associated with a shock.
- In front of the contact discontinuity, slow shock is formed.
- Fast expanding (rarefaction) wave is also formed to the low temperature
and low density side of the initial discontinuity of the gas fluid.
Please refer THIS document (PDF file in Japanese)
for detailed explanation.

Brio, M. & Wu, C. C. 1988, J. Comp. Phys., 75, 400
Ryu, D. & Jones, T. W. 1995 ApJ, 442, 228