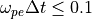電磁プラズマ粒子シミュレーション¶
- 著者:
松本洋介(千葉大学)
宇宙空間における爆発的現象に伴う、非熱的粒子の生成メカニズムは宇宙物理学に残された最大の問題の一つであると言えます。流体近似を行った磁気流体(MHD)シミュレーションでは、このような高エネルギー粒子生成メカニズムを自己無同着に理解することができないため、無衝突プラズマの第一原理計算手法によるアプローチが代わりに大きな役割を果たします。
本章では、そのような計算手法のひとつである、 電磁プラズマ粒子シミュレーション のアルゴリズムについて説明します。
概要¶
変数の定義¶
基礎方程式¶
基礎となる方程式系は、Vlasov方程式と
(1)¶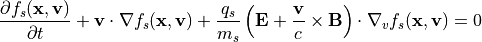
Maxwell方程式
(2)¶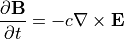
(3)¶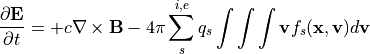
(4)¶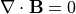
(5)¶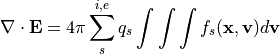
のVlasov-Maxwell方程式系です。式 (1) - (7) をカップルして解く無衝突プラズマの第一原理計算手法のうち、式 (1) の分布関数 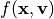 の時間発展を直接解く手法を電磁ブラソフシミュレーション、分布関数
の時間発展を直接解く手法を電磁ブラソフシミュレーション、分布関数 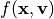 を粒子に代表させて解く手法を 電磁プラズマ粒子シミュレーション と呼びます。以下では、 電磁プラズマ粒子シミュレーション においてこれら方程式をどのようにして数値的に解いていくかを見ていきます。
を粒子に代表させて解く手法を 電磁プラズマ粒子シミュレーション と呼びます。以下では、 電磁プラズマ粒子シミュレーション においてこれら方程式をどのようにして数値的に解いていくかを見ていきます。
粒子と電磁場の時間発展¶
分布関数の位相空間上での時間発展は、実空間上の移流(移動、式 (1) の第2項)と速度空間上の移流(加速、式 (1) の第3項)の二つに分けて考えることができます [1] 。粒子シミュレーションではこれを、個々の粒子の運動を以下の様にして解くことにより、表現します。
加速:
(6)¶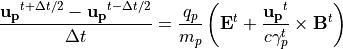
移動:
(7)¶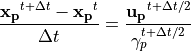
ここで、 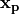 と
と 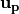 はそれぞれ粒子pの位置、4元速度を表し、各変数の右肩にある
はそれぞれ粒子pの位置、4元速度を表し、各変数の右肩にある 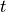 や、
や、 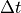 は、時刻とシミュレーションにおける時間刻み幅を表します。また、
は、時刻とシミュレーションにおける時間刻み幅を表します。また、 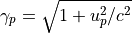 はローレンツ因子を表します。Maxwell方程式とは電流密度(式 (3) 右辺第2項)を通じてカップルします。電流密度は以下の様にして計算します。
はローレンツ因子を表します。Maxwell方程式とは電流密度(式 (3) 右辺第2項)を通じてカップルします。電流密度は以下の様にして計算します。
(8)¶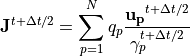
ここで、Nは対象となる粒子数を表します。上記電流密度を使うと結局、
(9)¶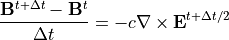
(10)¶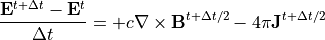
が粒子シミュレーションで解くべきMaxwell方程式となります。
時間更新手順¶
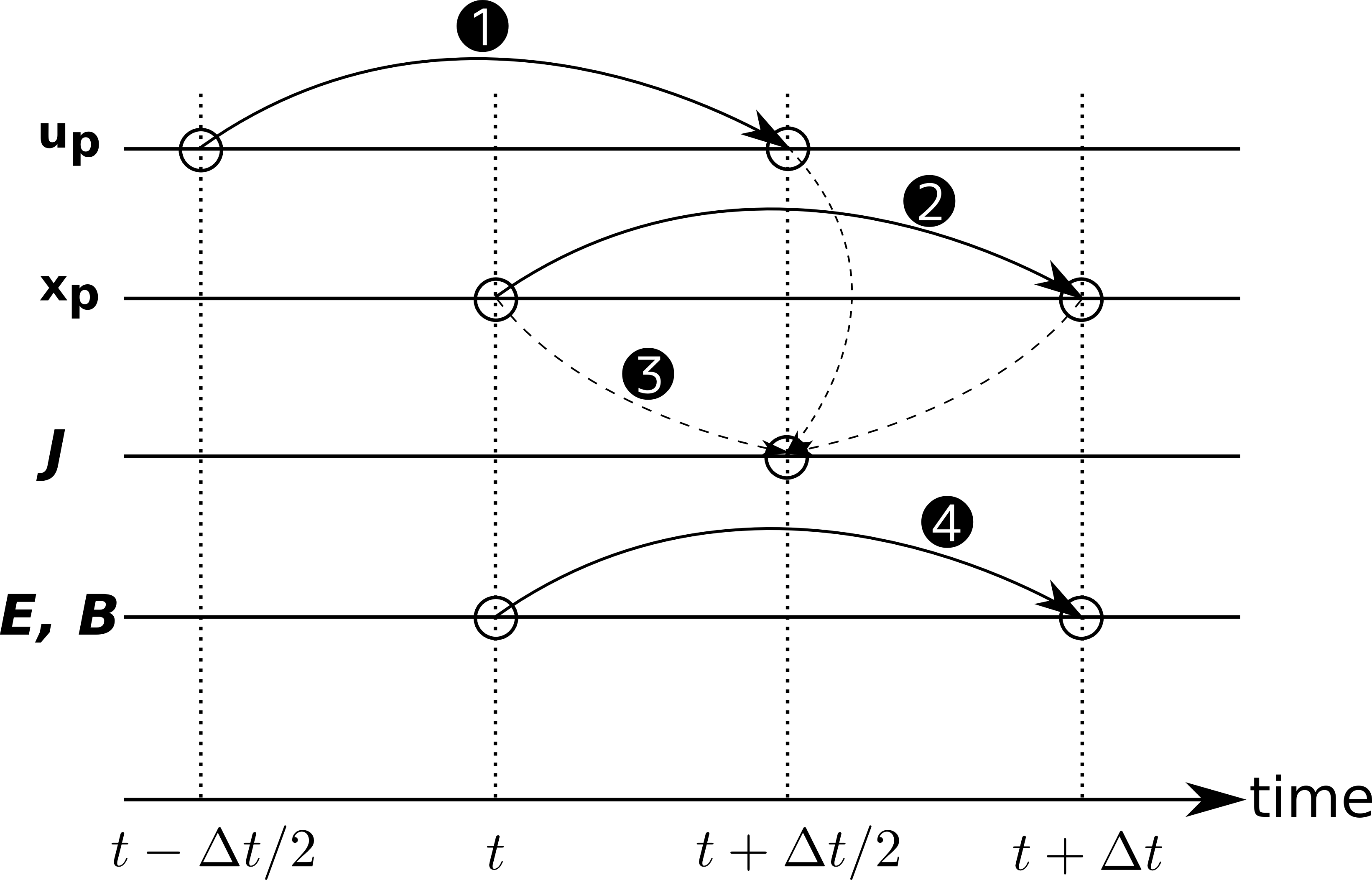
物理量の時間更新手順を 図 に示します。時間更新は、
粒子の速度を更新する(加速)
粒子の位置を更新する(移動)
半整数時刻における電流密度を、整数時刻の位置と半整数時刻の速度から計算する
電磁場を更新
1に戻る
のような手順で進めます。以下では、式 (4) と (7) を満たしながら、式 (6) - (10) をどのようにして解いていくかを具体的に見ていきます。
Footnotes
Buneman-Boris法¶
粒子の速度の時間更新は、式 (6) を元に行います。ここで 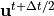 を求めるのに、
を求めるのに、 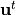 の情報が必要なことに注意してください。従って、時間更新に工夫が必要となります。以下では、プラズマ粒子シミュレーションにおける標準的アルゴリズムである、 Buneman-Boris法 について説明します。Buneman-Boris法では、粒子の加速を、電場による加速(速度空間上における移流)と、磁場による加速(速度空間上における回転)に分けて取り扱います。
の情報が必要なことに注意してください。従って、時間更新に工夫が必要となります。以下では、プラズマ粒子シミュレーションにおける標準的アルゴリズムである、 Buneman-Boris法 について説明します。Buneman-Boris法では、粒子の加速を、電場による加速(速度空間上における移流)と、磁場による加速(速度空間上における回転)に分けて取り扱います。
まず、以下のような変数を定義します。
(11)¶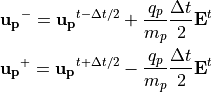
この新しい変数を用いて式 (6) を書き表すと、
(12)¶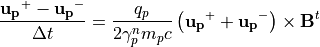
となります。ここで、式 (12) に 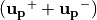 との内積を取ると、右辺は0となるので、その結果
との内積を取ると、右辺は0となるので、その結果 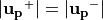 の関係が得られます。このことから、 Buneman-Boris法におけるベクトルの関係 のように、
の関係が得られます。このことから、 Buneman-Boris法におけるベクトルの関係 のように、 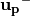 から
から 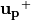 を求めるには、
を求めるには、 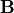 を軸として、
を軸として、 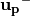 を角度
を角度 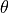 だけ回転させれば良いことがわかります。
だけ回転させれば良いことがわかります。
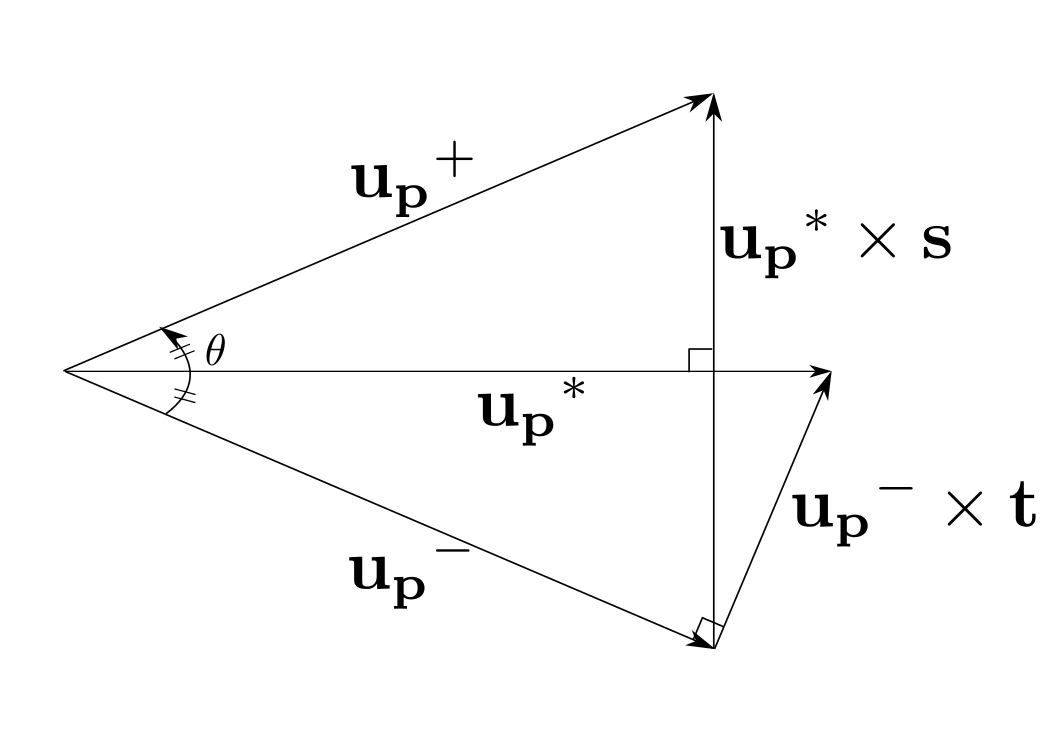
Buneman-Boris法におけるベクトルの関係¶
角度 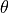 は
は
(13)¶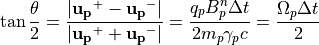
で与えられます。ここで、 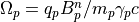 は粒子pのジャイロ周期を表します。これより角度
は粒子pのジャイロ周期を表します。これより角度 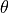 は、
は、
(14)¶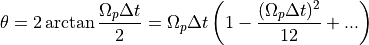
から求められ、時間2次精度でジャイロ運動を記述できることが分かります。
四則演算数を少なくするために、実際の計算では一度に角度 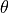 の回転を行わず、
の回転を行わず、
(15)¶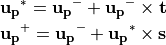
の2段階に分けて解くことを行なっています。ここで  と
と  はそれぞれ、
はそれぞれ、
(16)¶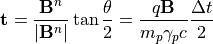
(17)¶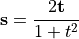
で与えられます( Buneman-Boris法におけるベクトルの関係 )。
以上をまとめると、粒子の加速は
電場による加速
(18)¶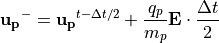
磁場による加速(回転)
(19)¶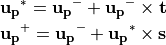
電場による加速
(20)¶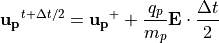
の3段階で行います。
最後に、粒子の位置を更新は、式 (7) を
(21)¶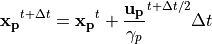
によって解くことにより行います。
Particle-in-Cell法¶
粒子の運動を解く上で(式 (18) - (20) )、粒子の位置における電磁場の情報が必要となります。電磁プラズマ粒子シミュレーションにおいて、粒子はシミュレーション空間内の任意の位置に存在するのに対して、電磁場は、 下記 で示すように、空間内のグリッド点上に定義されています。また、式 (8) や 下記 で示す電磁場の時間発展を解く際には、逆にグリッド点での電流密度の情報が必要となります。粒子シミュレーションでは、ラグランジュ量である粒子とオイラー量である(電磁)場を、粒子を質点ではなく有限の広がりを持った 超粒子 として扱うことによって、結びつけます。
ここで1次元( 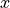 方向)の場合を例にとって、具体的な計算を見て行きましょう。粒子の位置
方向)の場合を例にとって、具体的な計算を見て行きましょう。粒子の位置 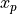 における場
における場 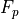 は、グリッド点
は、グリッド点 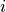 に定義されたの場
に定義されたの場 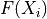 の情報を用いて
の情報を用いて
(22)¶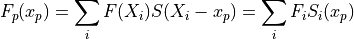
より求めます。ここで、 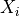 はグリッド点
はグリッド点 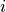 の位置を表します。また、
の位置を表します。また、 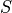 は粒子の形状関数(shape factor)と呼ばれるもので、ある粒子の位置(
は粒子の形状関数(shape factor)と呼ばれるもので、ある粒子の位置( 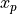 )からグリッド点に対して及ぼす影響度合い(重み)を表します。形状関数は、0次のnearest grid point(NGP)法、 1次の cloud in cell (CIC) 法が広く使われています。また近年では、2次のスプラインを用いた、よりノイズが少ない手法も使われるようになってきました。それぞれの手法に対応する形状関数を 各手法の形状関数 に示します。
)からグリッド点に対して及ぼす影響度合い(重み)を表します。形状関数は、0次のnearest grid point(NGP)法、 1次の cloud in cell (CIC) 法が広く使われています。また近年では、2次のスプラインを用いた、よりノイズが少ない手法も使われるようになってきました。それぞれの手法に対応する形状関数を 各手法の形状関数 に示します。
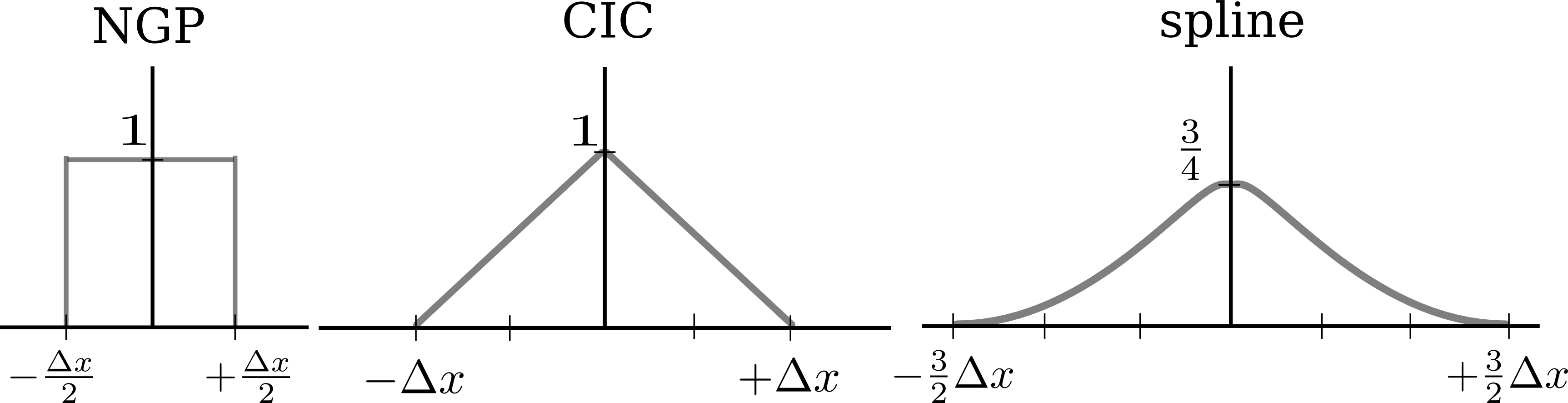
各手法の形状関数¶
NGPの形状関数は、
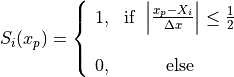
で表され、名前の通り、近接するグリッド点にのみ影響を及ぼす形状をしています。CIC法では、
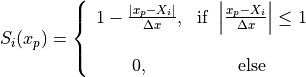
のように線形補間を行います。2次のスプラインの方法では、
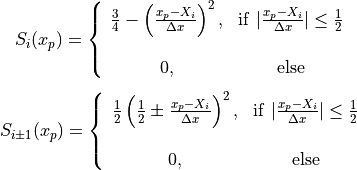
のような、なめらかな(微分が連続な)形状関数となっているため、ノイズを大きく減らすことができます。 pCANS では、1次元コードはCIC法を採用しており、多次元コードでは0−2次までの形状関数を選択できるようになっています。
グリッド点 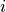 の電流密度を求めるには、逆に粒子の位置と速度から
の電流密度を求めるには、逆に粒子の位置と速度から
(23)¶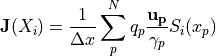
のようにして求めます。以上では1次元の計算を例に取って見てきましたが、多次元計算の場合は、
(24)¶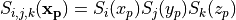
の様に、1次元の形状関数を掛け合わせることで求めることができます。
以上の様にして、粒子とグリッド点に定義される場をカップルさせる手法を一般に Particle-in-Cell法 と呼びます。
電磁場の数値解法¶
計算グリッド¶
電磁場は 電磁場の配置図 のように、シミュレーション空間内に定義されたグリッド点に配置されます。このような入れ子(スタッガード)格子を Yee格子 と呼びます。
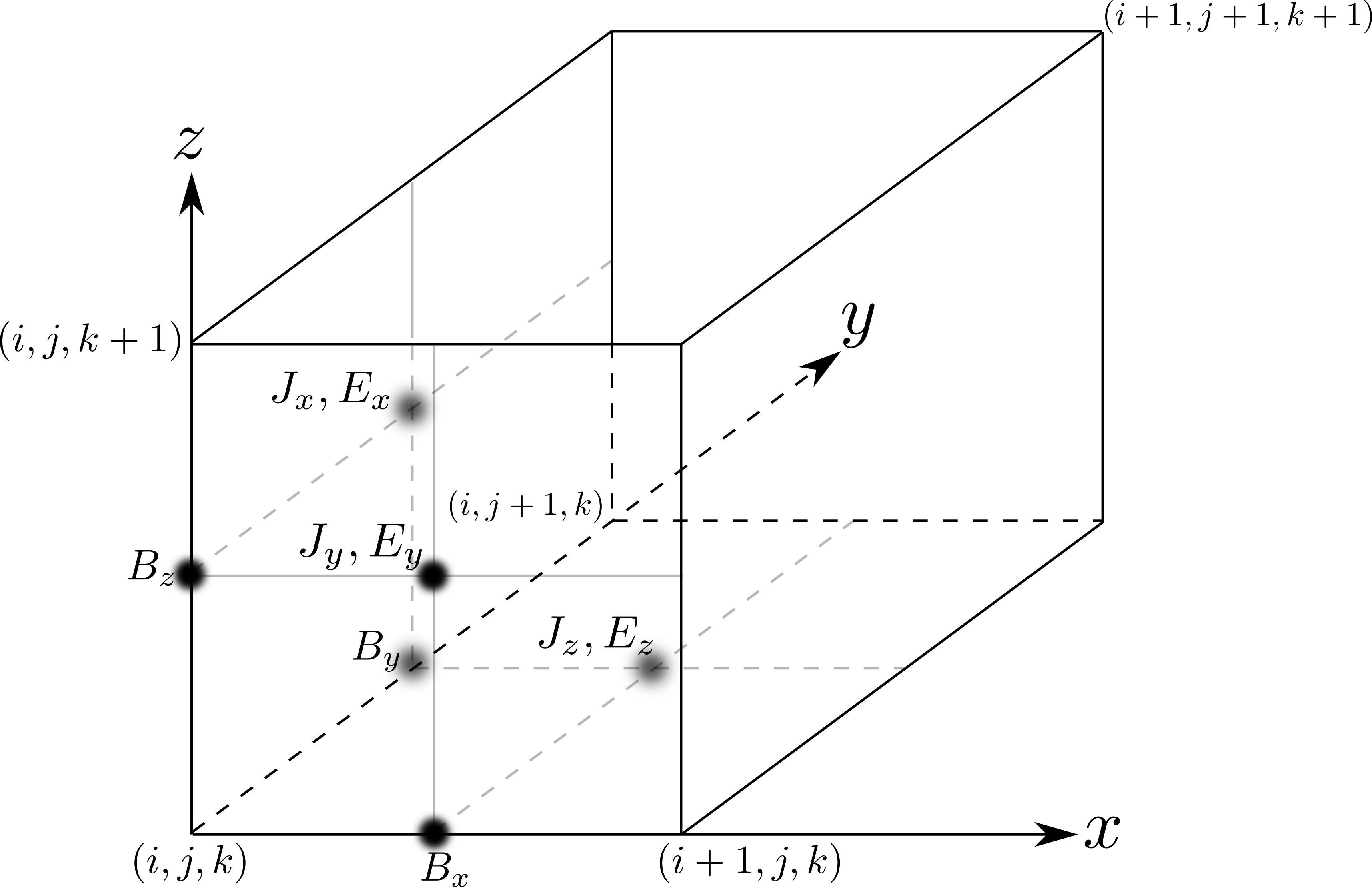
電磁場の配置図¶
このように電磁場を配置することにより、式 (4) を満たしつつ( 後述 )、空間2次精度で式 (9) , (10) の右辺を差分化して、表現することができます。 例えば、式 (9) の 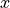 成分は
成分は
(25)¶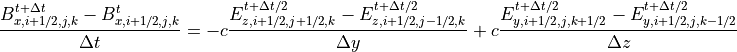
のようにして、差分化します。
陰的解法¶
次に、マクスウェル方程式 (9) , (10) の数値解法について説明します。真空中のマクスウェル方程式の数値解法のうち、Finite-Difference Time-Domain (FDTD) 法 ( Yee, 1966 )が標準的な解法として知られていますが、 pCANS では 星野 が開発した陰的解法を採用しています。本手法は、
CFL条件が光速cに縛られず、安定に解ける
電場と磁場を同じ時間ステップ上に定義できる
時間・空間2次精度(FDTD法と同じ)
という特徴がある一方、
反復法の導入
といった、新たな数値アルゴリズムが必要となります。そのため、陽解法より計算コストがかかりますが、電磁プラズマ粒子シミュレーションでは Particle-in-Cell法 が全計算コストの大部分を占めるため、それほど全体の計算コストを増やすことなく陰解法の安定性のメリットを享受できます [2] 。以下では本手法について説明します。
(26)¶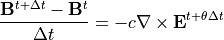
(27)¶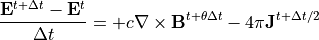
ここで、
(28)¶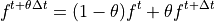
です。 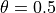 の場合は式 (9) , (10) に一致し、2次精度のクランク・ニコルソン法と呼ばれます。
の場合は式 (9) , (10) に一致し、2次精度のクランク・ニコルソン法と呼ばれます。 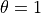 の場合は1次精度の後進オイラー法となります。 pCANS では
の場合は1次精度の後進オイラー法となります。 pCANS では 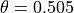 など、0.5より少し大きな値を使うことにより、適度に後進オイラーによる減衰効果を取り入れて、短波長ノイズを落としています。 式 (28) に従って式 (26) , (27) を変形すると、
など、0.5より少し大きな値を使うことにより、適度に後進オイラーによる減衰効果を取り入れて、短波長ノイズを落としています。 式 (28) に従って式 (26) , (27) を変形すると、
(29)¶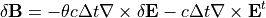
(30)¶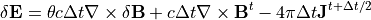
と、 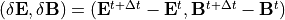 についての方程式が得られます。式 (30) に
についての方程式が得られます。式 (30) に 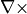 を作用させて、
を作用させて、 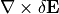 を式 (29) に代入して
を式 (29) に代入して 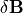 について整理すると、
について整理すると、
(31)¶![\left[1-\left( \theta c \Delta t \right)^2 \nabla^2 \right] {\bf \delta B} = \theta \left(c \Delta t \right)^2 \left( \nabla^2 {\bf B}^t + \frac{4\pi}{c} \nabla \times {\bf J}^{t+\Delta t/2} \right) -c \Delta t \nabla \times {\bf E}^t](_images/math/70b11a1fed9810c28cfba95a152af0881e902312.png)
となり、 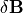 に対する方程式が得られます。ここで、右辺は既知量であることに注意してください。簡単のために、1次元計算(
に対する方程式が得られます。ここで、右辺は既知量であることに注意してください。簡単のために、1次元計算( 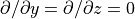 )を例にとってみましょう。グリッド点
)を例にとってみましょう。グリッド点 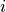 における式 (31) の磁場の一成分(
における式 (31) の磁場の一成分( 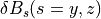 ,
, 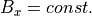 )に着目すると、
)に着目すると、
(32)¶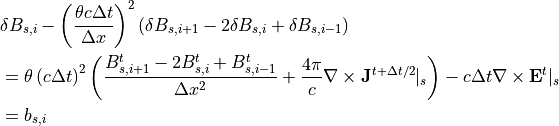
のように表されます。これは、
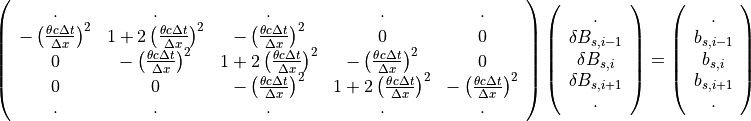
のように整理できます。シミュレーション領域の境界条件を与えると式 (32) は閉じて、結局、連立1次方程式
(33)¶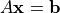
の形で表すことができます。式 (33) の解 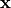 は
は 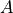 の逆行列
の逆行列 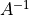 を作用させて
を作用させて
(34)¶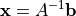
によって求めることができますが、通常 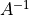 を解析的に求めるには大きな数値コストが必要となるため、反復法によって解を求めます。 pCANS ではKrylov部分空間法の一種である 共役勾配法(Conjugate Gradient method) と呼ばれる反復法を用いて式 (31) を解いています。特に、
を解析的に求めるには大きな数値コストが必要となるため、反復法によって解を求めます。 pCANS ではKrylov部分空間法の一種である 共役勾配法(Conjugate Gradient method) と呼ばれる反復法を用いて式 (31) を解いています。特に、 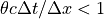 の場合は、Aは対角優勢な行列になるため、反復法における収束は少ない反復回数で実現されます。
の場合は、Aは対角優勢な行列になるため、反復法における収束は少ない反復回数で実現されます。 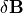 を求めた後、式 (30) に代入することによって、
を求めた後、式 (30) に代入することによって、 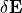 を得ることができます。
を得ることができます。
Footnotes
過去の情報から未来の値を推測する時間更新方法を 陽解法 と呼び、未来の情報も含めて推測する方法を 陰解法 と呼ぶ。
束縛条件を満たすために¶
電磁場を数値的に解くなかで、束縛条件である式 (4), (7) は必ずしも保証されておらず、その破れは数値的破綻をもたらします。以下では、これら束縛条件を満たしながら時間発展を行う方法につい説明します。
磁場の発散なし¶
電磁場を 電磁場の配置図 のように配置した場合、 (9) は2次元において、以下のように差分化できます。
(35)¶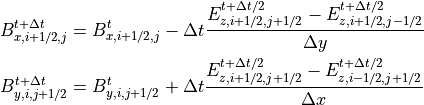
その結果、差分化した 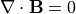 、つまり、
、つまり、
(36)¶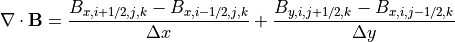
は時間更新前後で維持されることがわかります。これは、式 (35) の左辺を式 (36) に代入すると明らかで、式 (35) の右辺の電場が相殺することにより 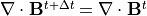 の関係が導かれます。従って、計算の初期条件(t=0)で
の関係が導かれます。従って、計算の初期条件(t=0)で 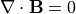 となっていれば、 差分化した
となっていれば、 差分化した 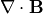 は計算の時間発展の間も丸め誤差の範囲で維持されます。
は計算の時間発展の間も丸め誤差の範囲で維持されます。
ガウスの法則¶
(37)¶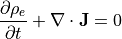
の、電荷保存則が得られます。PIC法で電荷密度を電流密度と独立に計算すると、必ずしも式 (37) を満たしているとは限らないため、 (静)電場に誤差が生じます。その誤差を少なく維持するために、式 (7) を満たすように電場を補正する手法がしばしば取られ、以下ではその補正方法を紹介します。式 (27) を解いた後の電場を 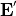 とし、ポアソン方程式
とし、ポアソン方程式
(38)¶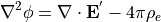
導入します。ここで、式 (38) 右辺は必ずしも  でないことに注意してください。これを 共役勾配法 などで解くことによって
でないことに注意してください。これを 共役勾配法 などで解くことによって 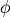 を求め、
を求め、
(39)¶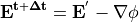
より電場の補正を行います。補正した電場は 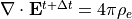 であることは明らかです。
であることは明らかです。
上記の電場補正方法では、PIC法により電荷密度を算出し、ポアソン方程式を解く必要が出てくるため、計算コストが増えます。これを回避するため、式 (37) を満たすような電流密度の計算方法が開発されており、この種の方法を電流密度計算における 電荷保存法 といいます。
電荷密度 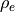 を半整数グリッド点に定義すると、式 (37) は(2次元の場合)、
を半整数グリッド点に定義すると、式 (37) は(2次元の場合)、
(40)¶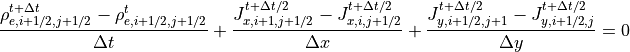
のように差分化することができます。これは 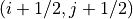 を中心としたセル内部の電荷の時間変化はセル表面から流入出する電荷フラックスによって変動すると考えられます。
を中心としたセル内部の電荷の時間変化はセル表面から流入出する電荷フラックスによって変動すると考えられます。
まず、粒子が時刻 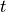 から
から 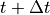 後に
後に 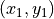 から
から 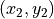 に移動したとします。また、
に移動したとします。また、
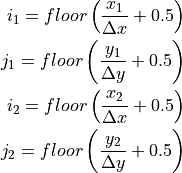
とします。ここで、floor(x)関数はxを越えない最大の整数を返します。粒子が 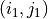 セル内に留まっている(
セル内に留まっている( 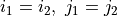 )場合、粒子がグリッド点に電流として寄与する量は、粒子の始点
)場合、粒子がグリッド点に電流として寄与する量は、粒子の始点 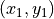 と終点
と終点 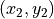 から以下のように計算することができます( Eastwood, 1995 )。
から以下のように計算することができます( Eastwood, 1995 )。
(41)¶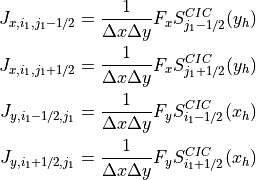
ここで、 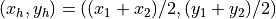 ,
, 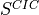 はCIC法の形状関数、
はCIC法の形状関数、 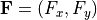 は
は
(42)¶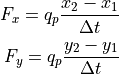
で与えられる電荷フラックスを表します。
以上では、同じセル内に留まっている場合のみを議論しましたが、一般には隣のセルに移ることも考えられます。その場合の取扱いの違いを 図 に示します。 Villasenor & Buneman (1992) では、始点と終点を直線で結び、図の場合、セル境界によって区切られた3つのセグメントそれぞれのセル内で上記の計算を行っています(Villasenor-Buneman法)。この場合、セル境界での交点を計算するのに分岐命令が多数必要となるため、計算コストが大きくなります。その問題を解消するために、 Umeda et al. (2003) は、 図 のように、途中で電荷密度が定義されるグリッド点を経由することでセル境界での交点の計算を少なくした方法を開発しています。この場合、軌道は直線とならないため、ジグザグ法と呼ばれています。一方、 Esirkepov (2001) は、 電荷を(2次元の場合)q/2の2つに分けて、それぞれの経路を直線で表す手法を開発しました。これを Density Decomposition法 と言います。本手法の利点として、
任意の次数の形状関数に対して同じアルゴリズムを適用できる(高次精度化が容易)
分岐処理が要らない
精度が良い
などが挙げられます。 pCANS の多次元コードでは、これら電荷保存法のうち Density Decomposition法 を採用し、 0から2次までの形状関数 を選ぶことができるようになっています。
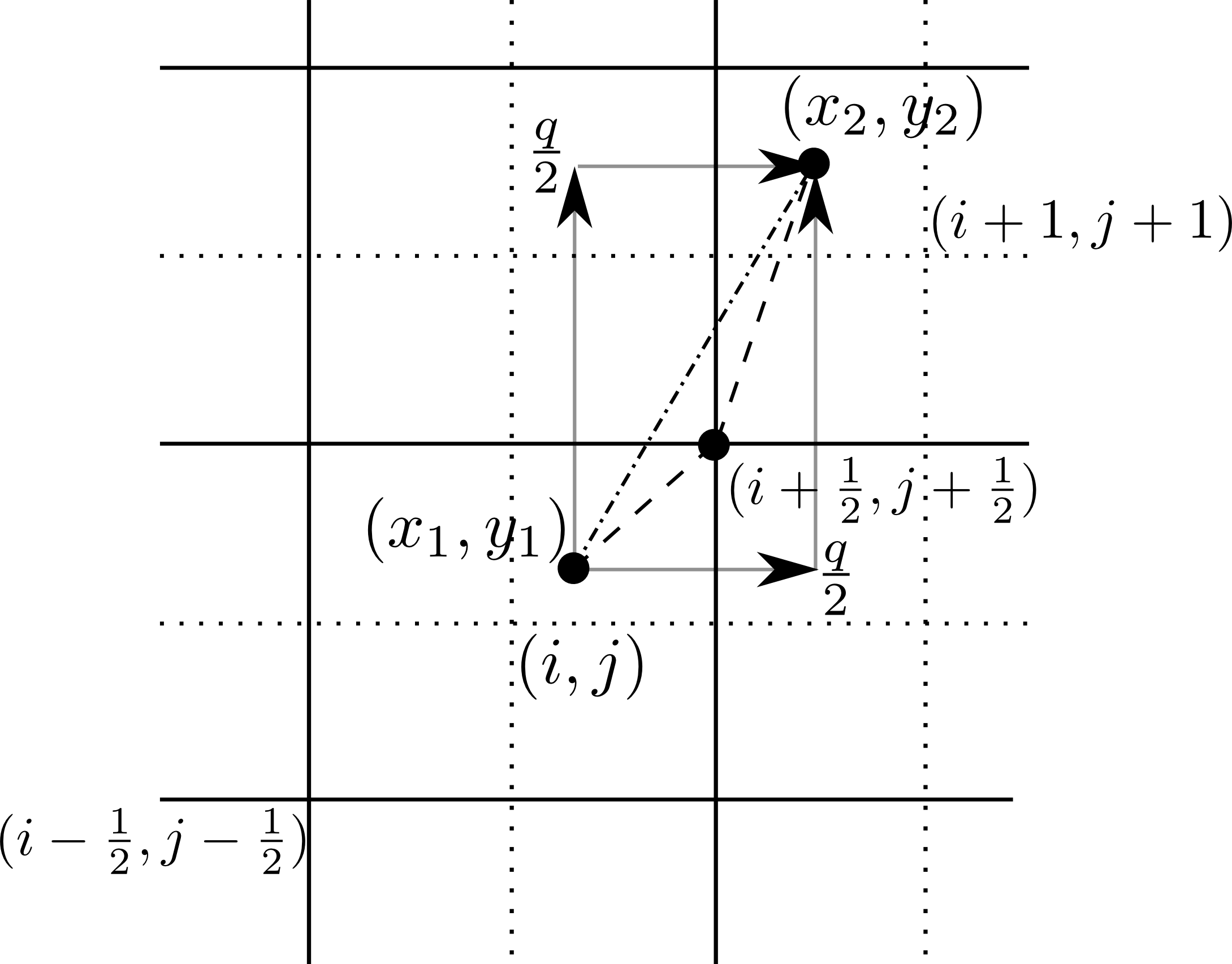
始点と終点を結ぶ軌道の扱いの違い。Villasenor-Bunemanの方法(一点破線線)では直線で結び、ジグザグ法(破線)では、電荷密度が定義されるグリッド点を経由する。Density Decomposition法(実線)では電荷を分け、それぞれに対応する経路で計算する。¶
パラメタの決め方¶
パラメタの決め方は各自の流儀によりますが、以下では pCANS での標準的な決め方を紹介します。
規格化定数:
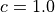
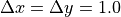 (グリッド幅)
(グリッド幅)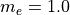 (電子静止質量)
(電子静止質量)
与えるパラメタ:
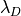 (デバイ長)
(デバイ長)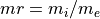 (イオン・電子質量比)
(イオン・電子質量比)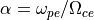 (電子プラズマ・ジャイロ振動数比)
(電子プラズマ・ジャイロ振動数比)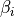 (イオンプラズマベータ、圧力と磁気圧の比)
(イオンプラズマベータ、圧力と磁気圧の比)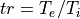 (電子・イオン温度比)
(電子・イオン温度比)
以上より、
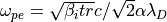
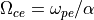
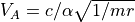 (アルヴェン速度)
(アルヴェン速度)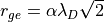
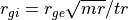
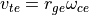
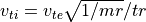
のようにして決めます。
空間・時間グリッド幅の決め方¶
通常、空間グリッド幅はデバイ長程度にとります。また、 pCANS は陰的解法を電磁場解法として採用しているので、光速によるCFL条件はありません。したがって、時間ステップ幅は粒子の運動から決まり、通常プラズマ振動を記述できるくらいの時間ステップ幅を採用します。典型的には、
のように選びます。
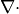 を作用させて
を作用させて