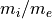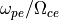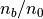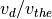電子-電子 静電2流体不安定性

著者:

天野孝伸（東京大学）

背景

2流体不安定性は無衝突プラズマの不安定性の中でも最も基本的なものである。無衝突系では異なる2つの領域が接しているような場合に、起源の異なる粒子分布が空間的に共存することが可能である。しかし粒子分布が相対速度を持っている場合には2流体不安定性を励起し、最終的には両者が混ざり合うことがあり得る。一口に2流体不安定性と言ってもパラメータによって不安定性の特徴は大きく異なることが知られているが、ここでは最も簡単な例として静電的な電子の2流体不安定性を考える。

初期条件

2つの電子流体（ビーム成分とコア成分）が磁力線方向(x方向とする）に相対速度を持って運動しており、また背景には静止した有限質量のイオンが存在している状態を考える。初期設定で用いるパラメータは以下の通りである。

m_i/m_e

100

\omega_{pe}/\Omega_{ce}

10

n_b/n_0

0.5

v_d/v_{the}

20.0

v_{the}

1.0

v_{thi}

1.0

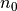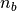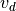ここで n_0 、 n_b 、 v_d はそれぞれ全密度、ビーム成分（正の方向に運動する成分）の密度、ビームとコア成分間の相対速度である。ここでは全体の運動量が0となる系を用いて計算を行うことにし、シミュレーション系での初期のドリフト速度は 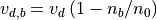v_{d,b} = v_d \left(1 - n_b/n_0\right) (ビーム成分)、 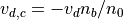v_{d,c} = -v_d n_b/n_0 （コア成分）とそれぞれ表される。なお各成分の初期の速度分布はマクスウェル分布とする。またグリッドサイズはデバイ長と等しくとり、グリッド数は512とする。

線形成長

今相対速度が熱速度に対して十分大きいと仮定すると分散関係は

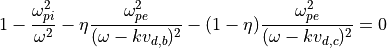
1 - \frac{\omega_{pi}^2}{\omega^2} - \eta \frac{\omega_{pe}^2}{(\omega - k v_{d,b})^2} - (1-\eta) \frac{\omega_{pe}^2}{(\omega - k v_{d,c})^2} = 0

のように書け、不安定解はこの分散関係の複素数解として得られる。ただし 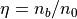\eta = n_b/n_0 と置いた。初期設定で用いる 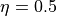\eta = 0.5 の時、最大成長率 \gamma_{\rm max} とその時の波数 k_{\rm max} は近似的に

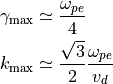
\gamma_{\rm max} & \simeq \frac{\omega_{pe}}{4} \\ k_{\rm max} & \simeq \frac{\sqrt{3}}{2} \frac{\omega_{pe}}{v_d}

と書くことができる。より正確な成長率と波数の関係を求めるには運動論的な分散関係を数値的に解く必要があるが、その結果を以下に図示する。

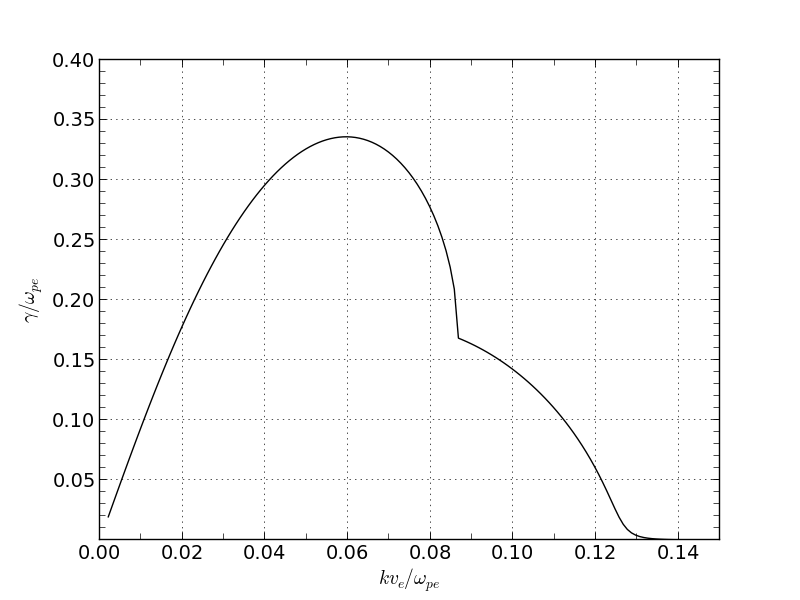
_images/ebeam_linear.png

運動論効果を考慮した不安定性の成長率の波数依存性。

以下の図ではシミュレーションから得られた電場の成長曲線と理論的な線形成長率とを比較している。ここでは電場を空間方向にフーリエ展開し、最大成長率近傍のモード4および5を比較している。この図から数値シミュレーションと線形理論の結果は非常に良く一致することが分かる。

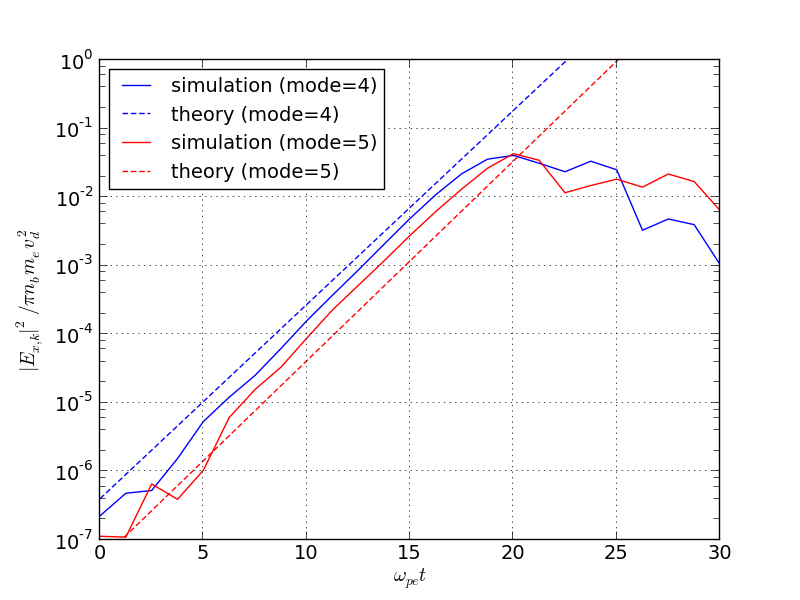
_images/ebeam_history.png

シミュレーションによって得られた成長曲線と線形成長率の比較。

飽和段階

この不安定性の成長率は非常に大きく、時刻 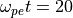\omega_{pe} t = 20 頃には非線形効果が効き飽和段階に入っている。以下の図では飽和段階における電子の位相空間分布を示している。この図から電子分布が渦状の構造をしていることが良く分かるが、これは不安定性で励起された静電ポテンシャルによって電子が捕捉されることからこのような構造ができると考えられている。この時の位相空間ホールに対応する電場構造は特徴的な双極的構造をしているが、類似の波形が地球磁気圏をはじめとして様々な領域で観測されている。これは実際に宇宙プラズマ中でこのようなホール構造が生成されていることを強く示唆する。

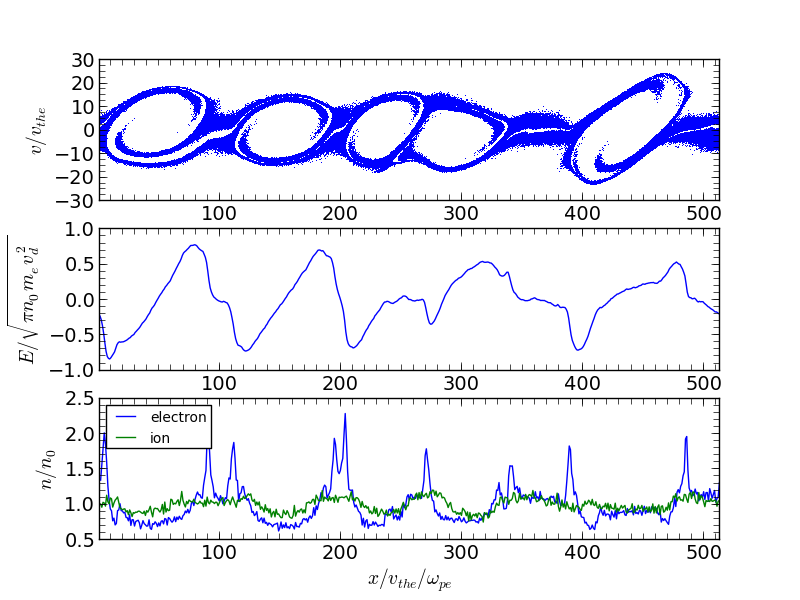
_images/ebeam_saturation.png

時刻 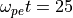\omega_{pe} t = 25 における電子の位相空間図、電場と密度。

非線形発展

飽和後十分に時間が経った後の位相空間図、電場と密度を以下に示す。この時点でもまたホール構造は維持されており、それに対応して双極型の電場構造も見て取ることができる。このホール構造は時間発展に伴い合体して、少数の大きなホール構造へと進化する。このような位相空間のホール構造はBGKモードと呼ばれる1次元のVlasov-Poisson方程式系の非線形厳密解であることが知られている。

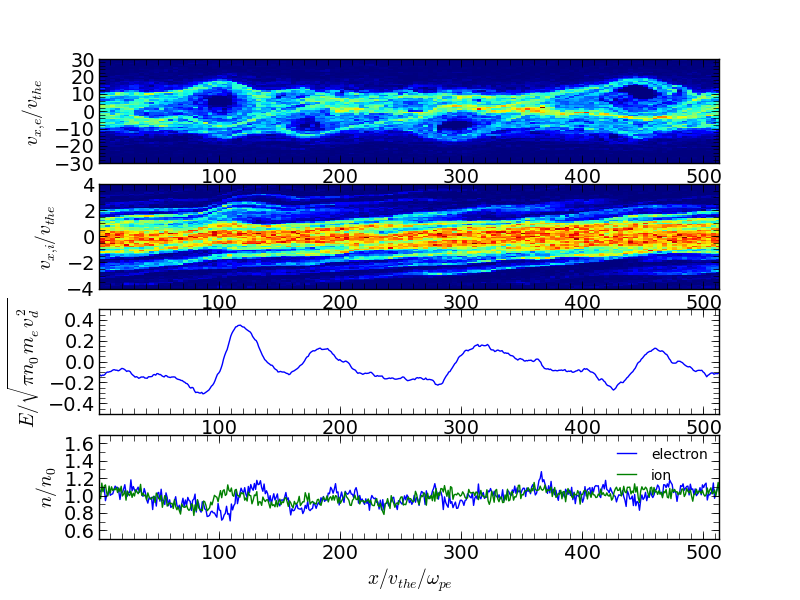
_images/ebeam_longterm1.png

時刻 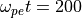\omega_{pe} t = 200 における電子・イオンの位相空間図、電場と密度。

パラメータ依存性

この不安定性はパラメータによってその線形・非線形発展の性質が大きく変わることが知られている。例えば以下の例ではイオンの温度を初期設定の1/100とした場合 (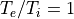T_e/T_i = 1) の計算例を示している。線形の時間発展にはほとんど初期設定の場合と違いが無いが、非線形発展の結果は大きく異なり、位相空間ホールの構造がほとんど見られない。一方で密度揺らぎの振幅が非常に大きくなっていることが分かる。これは不安定性によって励起されたBGKモード(Langmuir波)がイオン音波に崩壊するためであると考えられている。イオン音波のLandau減衰率は電子とイオンの温度比に大きく依存することから、このような大きな非線形発展の違いが現れる(Omura et al. 1996)。

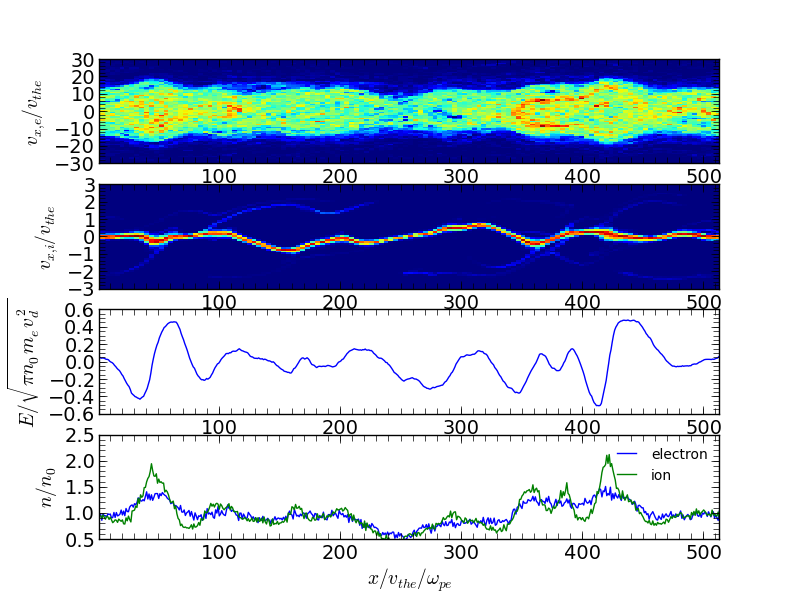
_images/ebeam_longterm2.png

上図と同様（ただし 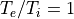T_e/T_i = 1 の場合）

参考文献