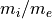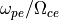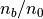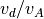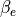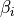電磁イオンサイクロトロン不安定性

著者:

天野孝伸（東京大学）

背景

電子-電子 静電2流体不安定性 の場合と同様にイオンの熱的成分（コア成分）とビーム成分が共存するような系を考える。この時もパラメータに寄って様々な異なる種類の不安定性が励起され得るが、ここでは磁力線並行方向にAlfven速度の数倍程度の速度で運動するイオンビームが励起する電磁イオンサイクロトロン不安定性(e.g., Winske & Leroy, 1984, Hoshino & Terasawa, 1985)を考える。この時はビーム成分のサイクロトロン共鳴によって右円偏波のAlfven波(whistler波)が励起されることが知られている。なお、この不安定性は衝撃波の前面や地球磁気圏のプラズマシートなど様々な場所において重要な役割を果たすと考えられている。

初期条件

初期設定では以下のようなパラメータを用いる。

m_i/m_e

25

\omega_{pe}/\Omega_{ce}

5

n_b/n_0

0.2

v_d/v_{A}

3.0

\beta_{e}

0.5

\beta_{i}

0.03125

電子-電子 静電2流体不安定性 との違いは電子は1成分であり、イオンが2成分になっているところだけである。グリッドサイズはデバイ長と等しくとり、グリッド数を1024とする。これにより系のサイズは 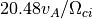20.48 v_{A}/\Omega_{ci} となる。

線形成長

磁力線方向に伝搬する右円偏波の電磁波の分散関係式は

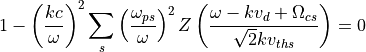
1 - \left(\frac{k c}{\omega}\right)^2 \sum_{s} \left(\frac{\omega_{ps}}{\omega}\right)^2 Z\left(\frac{\omega - k v_d + \Omega_{cs}}{\sqrt{2} k v_{ths}}\right) = 0

で表される。ただし 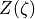Z(\zeta) はプラズマ分散関数を表す。この式にシミュレーションで用いる値を代入し、線形成長率を数値的に求めた結果を以下に図示する。ここからこの不安定性は波数 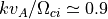k v_{A}/\Omega_{ci} \simeq 0.9 付近で成長率が最大となり、最大成長率は 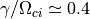\gamma / \Omega_{ci} \simeq 0.4 程度であることが分かる。

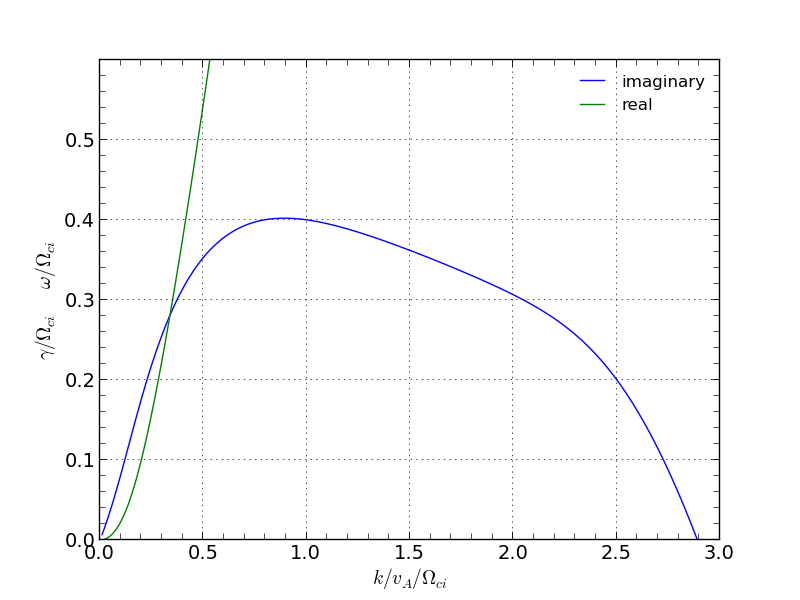
_images/ibeam_linear.png

不安定性の成長率と周波数の実部。

以下の図ではシミュレーションから得られた磁場の横波成分の振幅の時間発展を線形理論と比較している。ただし、右回り成分と左回り成分を分離するために複素数 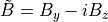\tilde B = B_y - i B_z を作り、これを空間方向にフーリエ展開した各モードの時間発展を示してある。線形理論の予測は数値シミュレーション結果を非常に良く再現していることが分かる。

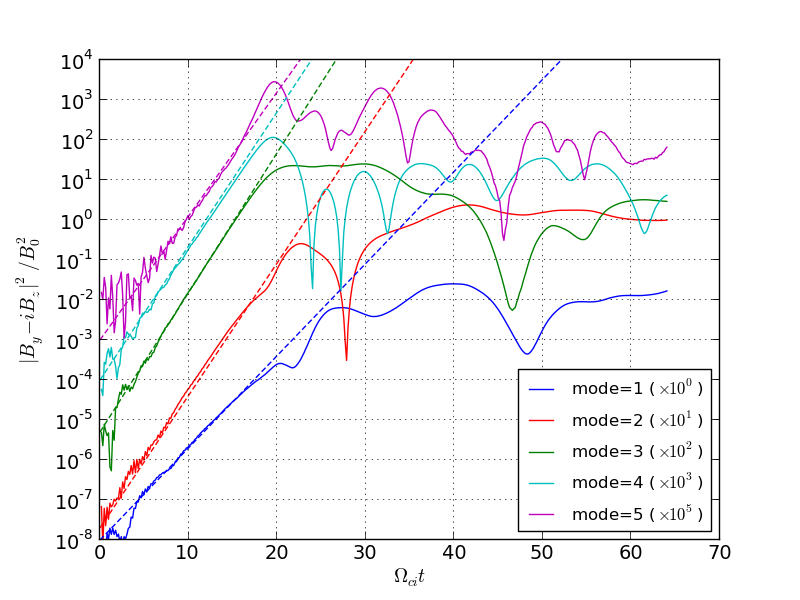
_images/ibeam_history.png

シミュレーションによって得られた成長曲線と線形成長率の比較。ただし見やすいように各モードを適宜上下にずらして表示してある。

速度分布関数の時間発展

不安定性により成長するAlfven波によって、やがてビーム成分はピッチ角散乱を受けるようになる。単色のAlfven波の中で運動するテスト粒子の運動を考えると、波と共に運動する系では波の電場が消えることから、波の静止系では粒子のエネルギーは保存する。従って粒子のピッチ角散乱は等エネルギー線に沿って起きることになる。

以下にはシミュレーションで得られたイオンの分布関数 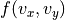f(v_x, v_y) の分布を示す。ただしここで 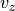v_z 方向には積分してある。不安定性が飽和したすぐ後の 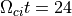\Omega_{ci} t = 24 の分布では確かにイオンビーム成分がピッチ角散乱によって三日月型の形状に変形されていることが分かる。その後は波動が単色波でないことや、非線形発展の影響が強く効くことから、より複雑な散乱過程を経ているものと思われる。

_images/ibeam_scatter.png

粒子の速度分布関数の発展の様子。等高線はログスケールで等間隔に表示している。

非線形発展

励起された波動の長時間発展は実際の問題への適用を考える際に非常に重要である。このシミュレーションでは観測されたAlfven波の振幅は背景磁場の強度と同程度にまで成長し、非線形性が大きく効いてくる。一般的に初期に単色波であったとしても、大振幅波動は非線形カップリングを通じて他の波動とエネルギーや運動量のやり取りをする。特に、ここで励起される円偏波のAlfven波については任意振幅の厳密解が存在するが、この解は不安定であることが良く知られている。このような不安定性はパラメトリック不安定性と呼ばれ、非線形性が強く効く宇宙プラズマでは重要になる局面が多い。

今のパラメータのようにイオン音波の位相速度がAlfven速度よりも遅い場合には特に減衰不安定性(decay instability)と呼ばれる不安定性が起こり、初期のAlfven波が同じ方向に進む短波長のイオン音波と逆向きに進む長波長のAlfven波へと分解する (e.g., Goldstein, 1978, Terasawa et al, 1986)。この過程が実際に起こっていることを下の図に示す。この時、親波のAlfven波と減衰不安定性によって作られる逆向きのAlfven波は周波数は同符号だが、空間的な回転方向（ヘリシティの符号）が逆になるためフーリエ展開することによって数学的に分離が可能である。この分解によって確かに逆向きに進む長波長の波が励起されていることが確認できる。

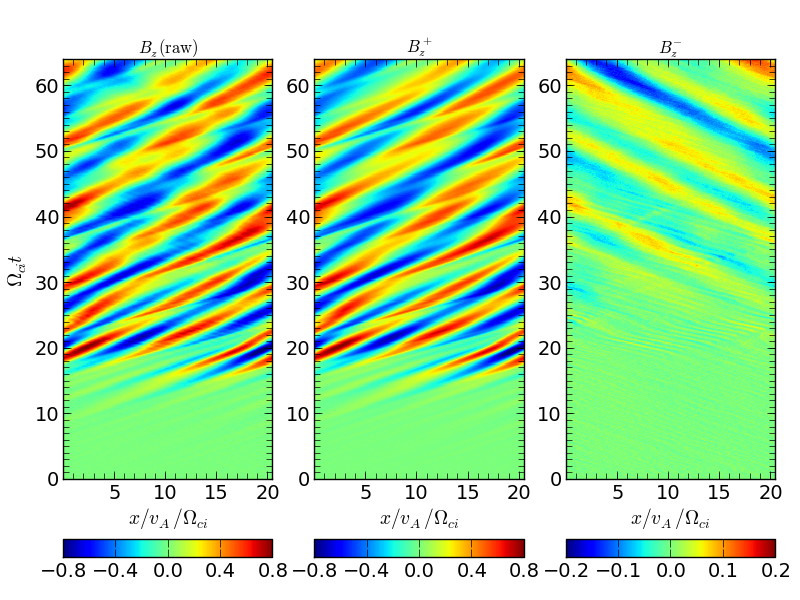
_images/ibeam_nonlinear.png

不安定性によって励起されたAlfven波の長時間発展。それぞれ(左)Bzの生の値、(中央)分解後のk>0、および(右)k < 0 のモード時間発展を示している。不安定性によって励起された右向きのAlfven波の振幅が大きくなるにつれて、左向きに進むより長波長のAlfven波が励起され始めることが分かる。

参考文献