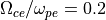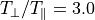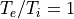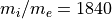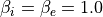電子温度異方性不安定

著者:

三好由純 (名古屋大学)、簑島敬（JAMSTEC）

背景

地球・惑星磁気圏では、しばしば磁力線に垂直方向の温度が平行方向の温度よりも卓越した分布関数が観測される。特にダイポール型の磁気圏において、荷電粒子の第一、第二断熱不変量が保存された状態で、粒子が磁場が強い惑星側に輸送された場合には、このような異方性を持った状態が自然に発達する。類似した磁場構造を持つ太陽コロナにおいても、フレアに伴って同様の分布関数が維持されていることが、電波観測から示唆されている。温度異方性(temperature anisotropy)と呼ばれるこのような分布がある場合には、イオンについては電磁イオンサイクロトロン波動を、電子についてはホイッスラーモード波動を励起することができる。粒子はこれらの波動と共鳴(ピッチ角散乱)して断熱不変量が破れ、ロスコーンの中に粒子が入り消失することも起こる。ここでは、そのような温度異方性を持った電子の分布を初期状態として与え、ホイッスラーモード波動が励起する様子を調べてみよう。なお、このホイッスラーモード波動は線形段階を経て非線形段階に入ると、コーラスと呼ばれる周波数がドリフトするような変化を示す。近年、このコーラス波動によって、地球磁気圏放射線帯の相対論的エネルギーの電子が加速されることが指摘され、注目を集めている。

線形成長率

温度異方性がある場合のホイッスラーモード波動の線形成長率は、Vlasov-Maxwell方程式を解くことによって得られる。 Kennel and Petschek (1966) は、温度異方性がある場合のホイッスラーモード波動を導いた。周波数 \omega_{r} と線形成長率 \omega_{i} はそれぞれ

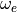(1)\omega_{r} &= \frac{k^2 c^2}{\omega_e^2 + k^2 c^2} \Omega_{e},\\ \omega_{i} &= \pi \Omega_{e} \left(1-\frac{\omega_{r}}{\Omega_e}\right)^2 \eta(V_{R}) \left[A(V_R)-A_c\right].

ここで、 \omega_e は電子プラズマ振動数、 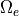\Omega_e は電子サイクロトロン振動数、

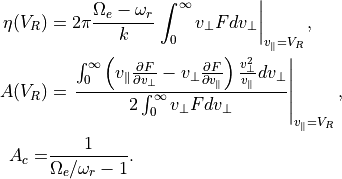
(2)\eta(V_{R}) &= 2 \pi \frac{\Omega_e-\omega_r}{k} \left. \int_{0}^{\infty} v_{\perp} F dv_{\perp} \right|_{v_{\parallel}=V_{R}},\\ A(V_{R}) &= \left. \frac{\int_{0}^{\infty} \left(v_{\parallel} \frac{\partial F}{\partial v_{\perp}} - v_{\perp} \frac{\partial F}{\partial v_{\parallel}} \right) \frac{v_{\perp}^2}{v_{\parallel}} dv_{\perp}}{2 \int_{0}^{\infty} v_{\perp} F dv_{\perp}} \right|_{v_{\parallel}=V_{R}},\\ A_c =& \frac{1}{\Omega_e/\omega_r - 1}.

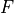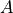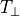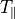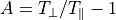もし、分布関数 F がマクスウェル分布の場合には、 A は垂直方向と平行方向の温度 T_{\perp} , T_{\parallel} を用いて、 A=T_{\perp}/T_{\parallel}-1 で与えられる。

線形成長率を計算した一例を 分散関係図 に示す。このとき、プラズマ周波数と電子サイクロトロン周波数の比は5、温度異方性 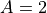A=2 である。

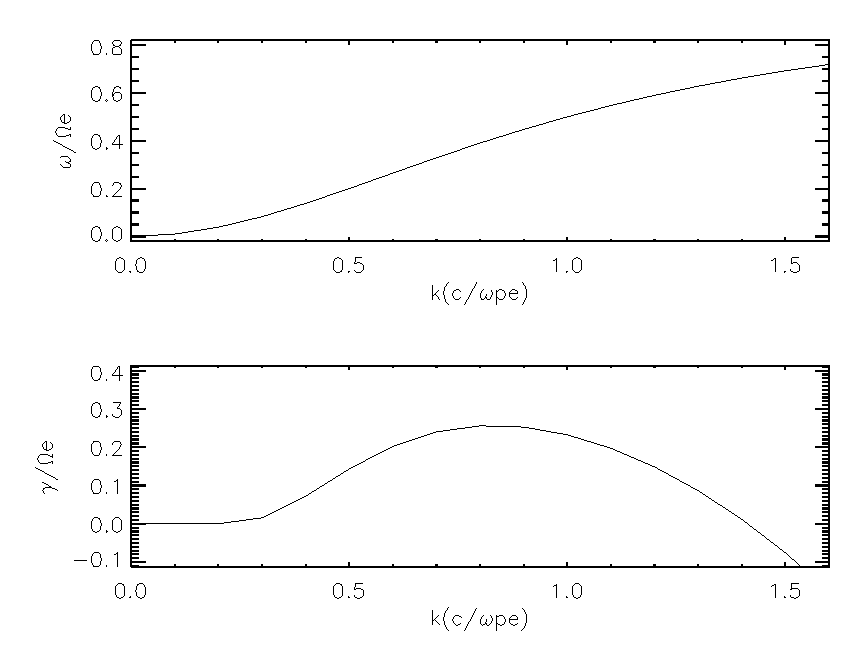
_images/whistler_dispersion.png

上：ホイッスラーモード波動の分散関係、下：線形成長率

計算例

初期条件として、 Sydora et al.(2007) をもとに、以下の初期条件で計算を行った。

  • \Omega_{ce} / \omega_{pe}=0.2

  • T_{\perp} / T_{\parallel}=3.0

  • T_{e} / T_{i} = 1

  • m_{i} / m_{e} = 1840

  • \beta_i = \beta_e = 1.0

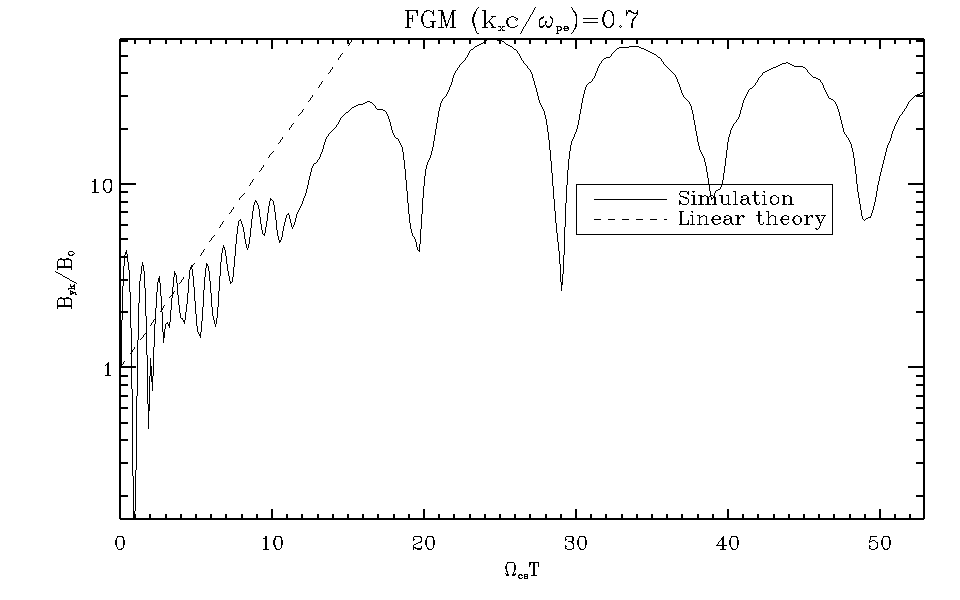
_images/whistler_k-t_fgm.png

最大成長モードのフーリエ振幅の時間変化（実線）と上記線形理論から求めた線形成長率（破線）との比較

フーリエ振幅の時間発展の図 では、シミュレーションで得られた最大成長率モード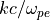（ kc/\omega_{pe} ）のフーリエ振幅(実線)の時間発展と線形成長率(破線)を比較している。線形段階においてシミュレーションと理論がよく一致していることがわかる。

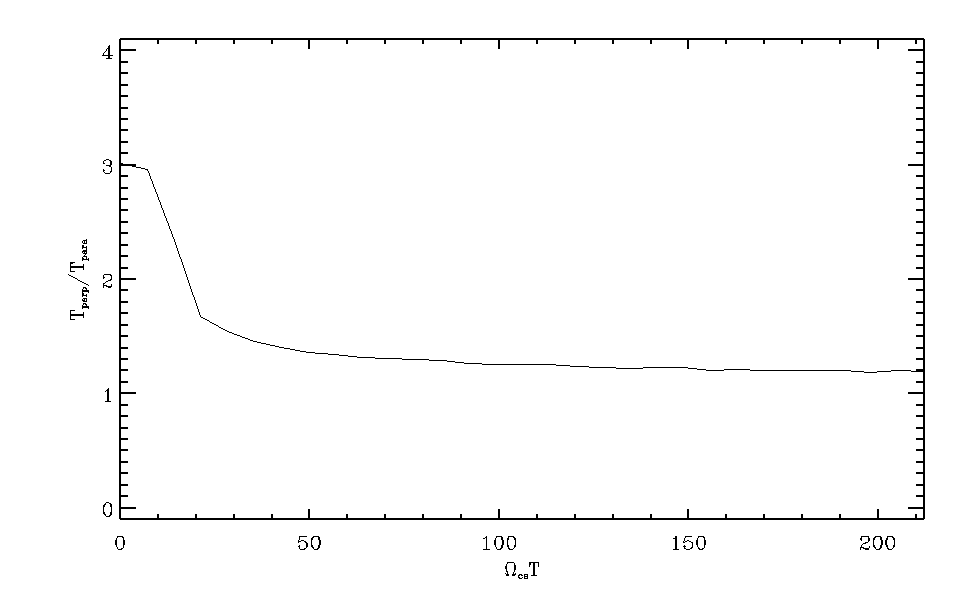
_images/whistler_t-tratio.png

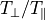T_{\perp}/T_{\parallel} の時間変化

波動を励起する自由エネルギーは分布関数の温度異方性であり、磁力線に垂直方向の温度が平行方向より高い場合に波動が励起する。 温度異方性の時間発展の図 では、電子の垂直温度と平行温度の比の時間変化を表している。波動の成長に伴って垂直温度と平行方向の温度の比が緩和される様子がわかる。飽和段階では温度比は約1.2となっている。

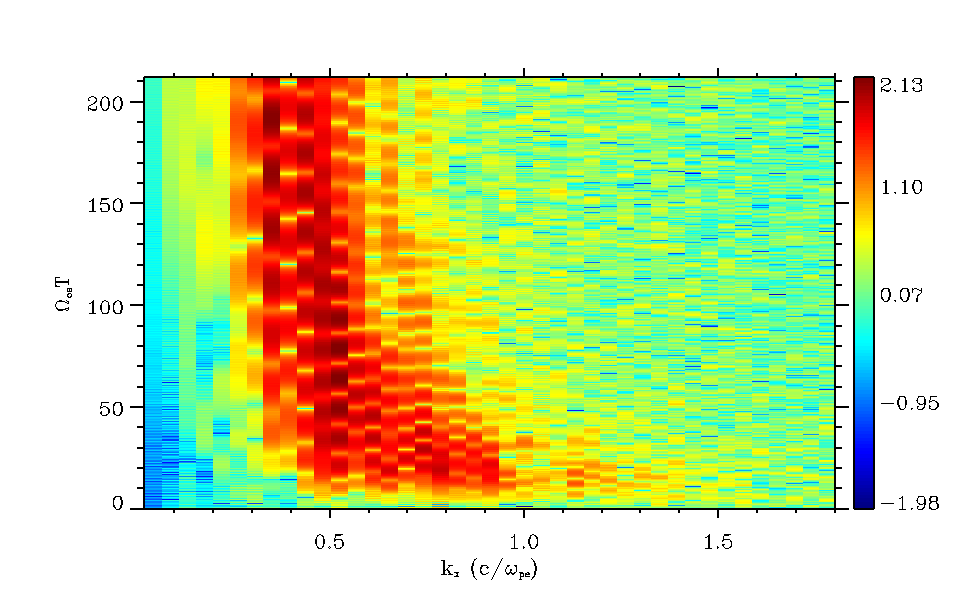
_images/whistler_k-t.png

波数スペクトルの時間変化

波数の時間変化図 はシミュレーションで得られた波数スペクトルの時間変化を示している。線形段階では 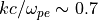kc/\omega_{pe} \sim 0.7 を中心とした波数帯に渡って波が励起され、それらは非線形段階では長波長モードへシフト(逆カスケード)している様子がわかる。これは、温度異方性の緩和に伴って、最大成長波長が長波長側にシフトするからだと考えられている（ Sydora et al., 2007 ）。

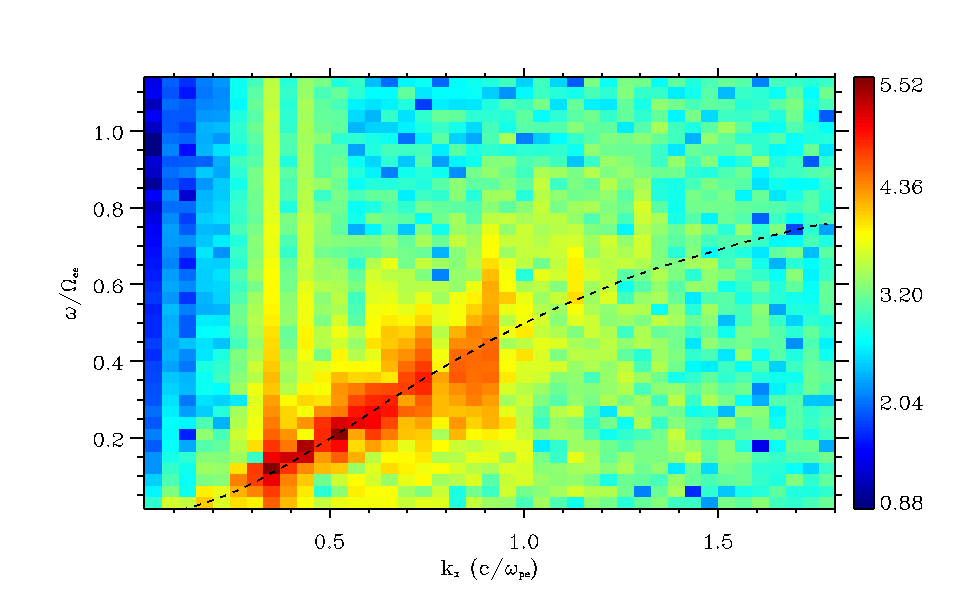
_images/whistler_k-w.png

電子温度異方性不安定によって励起された波の分散関係

分散関係の図 には、励起された波の分散関係を描いている。破線は低周波電磁モードのひとつであるRモード（ホイッスラー波）の分散関係を表している。これより、電子温度異方性不安定で励起される波は、ホイッスラー波であることが分かる。

参考文献