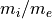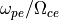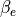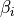無衝突衝撃波¶
- 著者:
天野孝伸（東京大学）
背景¶
無衝突プラズマ中に発生する無衝突衝撃波（ここでは速い磁気音波に対する衝撃波を考える）は非常に複雑な現象である。衝撃波は磁気音波モードの非線形波動であるため、急峻化によって短波長のモードを励起し、イオン慣性長程度で磁気音波の分散性が現れ急峻化と拮抗する。また磁場が圧縮されることから、波面に強い電流が流れ、これが様々な不安定性を介して（異常抵抗による）散逸を引き起こす。しかし、ある程度強い衝撃波ではこれらの過程では十分な散逸を引き起こすことができず、実効的な粘性が必要となってくる。無衝突衝撃波ではこの粘性を担うのが反射イオンであると考えられている。反射イオンは自分自身の加速や不安定性の励起を通してマクロな散逸を引き起こすが、その詳細な過程はパラメータによって大きく異なる。以下で見るように、特にマッハ数や衝撃波角（衝撃波の法線と上流の磁場のなす角度）の違いによってこの差は非常に顕著となることが知られている。このようにパラメータによって異なる複雑な挙動を示す高度に非線形な現象である無衝突衝撃波はプラズマ理論の実験室として非常に有用であった。
またもう一つの重要な側面として無衝突衝撃波が粒子の加速器として働くことが挙げられる。特に最近では超新星残骸をはじめとする天体衝撃波への応用として研究されることが多くなってきている。特に地球磁気圏前面の定在衝撃波（バウショック）や惑星間空間衝撃波の人工衛星による直接観測は衝撃波の運動論的な数値シミュレーションと共に1970年代後半に確立した1次Fermi加速理論の実証に非常に重要な役割を果たしてきた。最近では電子スケールからイオンスケールやMHDスケールに至るまでを運動論的な数値シミュレーションによって自己無撞着に解き明かそうという試みが今まさに進行中である。
以下では無衝突衝撃波を理解するにあたって必要な基礎的な事項を数値シミュレーション結果を通して見ていくことにする。
垂直衝撃波と反射イオン¶
無衝突衝撃波の性質は衝撃波角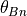 
で大きく変わることから、一般的に衝撃波角の値によってその呼び名が変わり、 通常45度以下の場合を準平行衝撃波、45度以上の場合を準垂直衝撃波、特に90度の場合を垂直衝撃波と呼んでいる。初期設定では最も簡単な状況として垂直衝撃波を扱っている。シミュレーションで用いた他のパラメータは以下の通りである。
25
5
90
3.0
0.5
0.125
ただしグリッドサイズは上流の電子デバイ長と等しくとり、グリッド数は2048としている。なお、マッハ数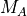 
はシミュレーション系での上流速度に対応するマッハ数である。ここではシミュレーション系は下流の静止系であるため、衝撃波静止系でのマッハ数はこれよりも大きな値となる。
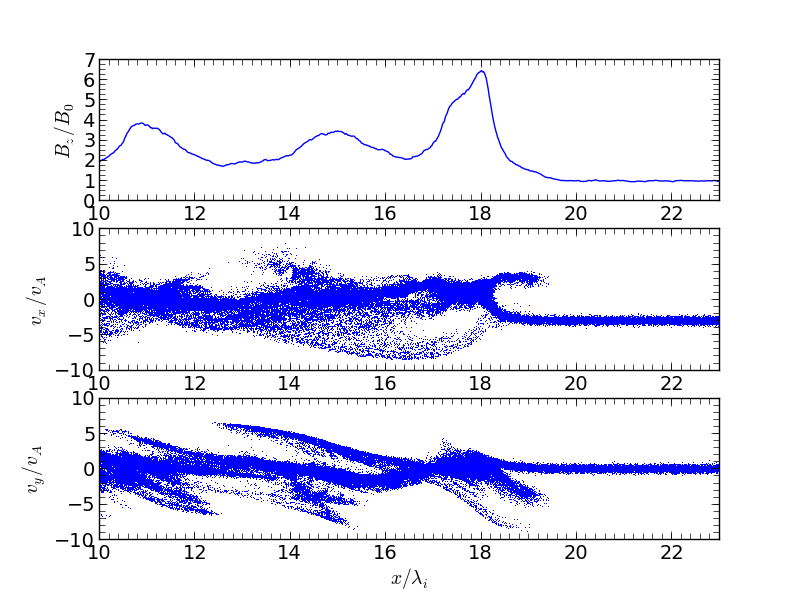
垂直衝撃波の構造(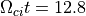 
)。¶
上図にはシミュレーション結果のスナップショットを示している。この図から分かるように、右側（上流側）から入射してくるイオンの一部が衝撃波面(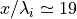 
)で反射されている。反射されたイオンは上流の電場 
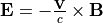によってy方向に強く加速され、衝撃波下流に抜けていく。この強く加速された反射イオンがRankine-Hugoniot関係式から要請される下流の圧力を担っていると考えれば良い。反射イオンの存在によって磁場が少し圧縮を受けている領域はfoot、磁場が急峻に立ち上がる領域はrampと呼ばれる。またramp以降で磁場強度は一定とはならずに振動しているため、磁場の大きな領域をovershoot、小さな領域をundershootと呼んでいる。これが垂直衝撃波の基本的構造であり、反射イオンがその構造を支配していることから、反射イオンのジャイロ半径が空間スケールを特徴づけている (Leroy, 1981, Leroy, 1982, Wu et al, 1984)。
衝撃波の非定常性¶
上で見たような衝撃波構造は必ずしも定常的な構造であるとは限らず、しばしば衝撃波は非定常な振る舞いをすることが知られており (e.g., Quest 1986)、この計算例においても実際に非定常性が見て取れる。下図にはシミュレーションから得られた磁場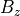 
の値を各時間ごとに上にずらしながらプロットしたものである。衝撃波は平均的に右側に進んでいるが、その構造は周期的に変化していることが分かる。
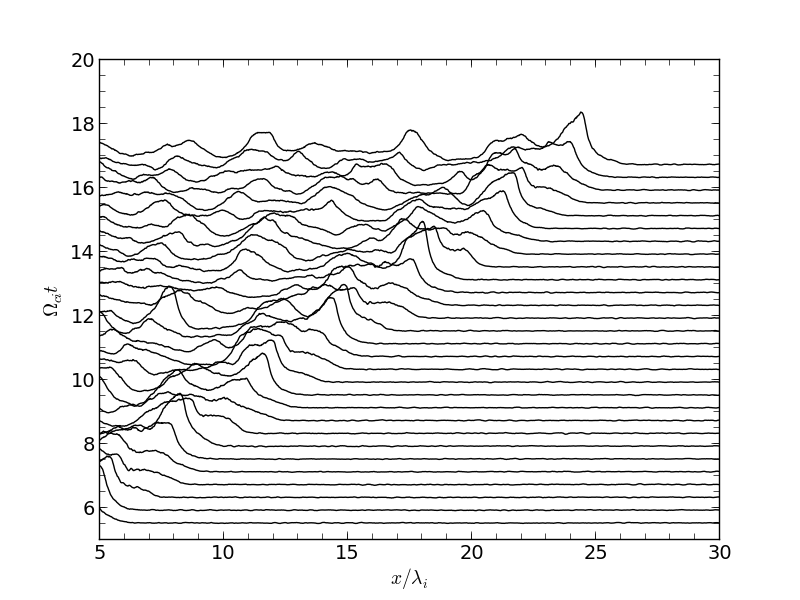
垂直衝撃波( )の時間発展。¶
この場合では衝撃波のfoot領域で磁場が次第に強くなり、そこに新しいramp構造が現れる。このような振る舞いを衝撃波の再形成(reformation)と呼んでいる。衝撃波の非定常性の議論は現在でも混沌としているため詳細には立ち入らないが、パラメータによってその振る舞いが異なることが知られている。例えばこの例で見られるような再形成は顕著でなくとも、例えばovershootの磁場強度が時間的に振動するような例も多くみられる。また反射イオンが励起する不安定性によって非定常性が影響を受ける可能性などについても議論されている。ただし筆者の私見では1次元計算では電流方向の自由度が無く、異常抵抗が含まれていないため、非定常性について最終的な結論を出すことはできないと考える。一方で多次元ではripplingと呼ばれる非定常性が存在するが (e.g., Winske & Quest 1988)、現状ではripplingと再形成との関係性についてはあまり理解されていない。
衝撃波角の依存性（準平行衝撃波）¶
既に述べたように衝撃波の構造は衝撃波角およびマッハ数に非常に大きく影響を受ける。ここでは例として衝撃波角を30度とした場合の準平行衝撃波の計算例を示す。ただし準平行衝撃波は時間・空間スケール共に準垂直衝撃波に比べて長くなるため、シミュレーション空間を広く、また積分時間も長くとる必要がある。従ってここではグリッド数は8096とし、200000ステップの計算を行った。以下に衝撃波構造のスナップショットを示す。
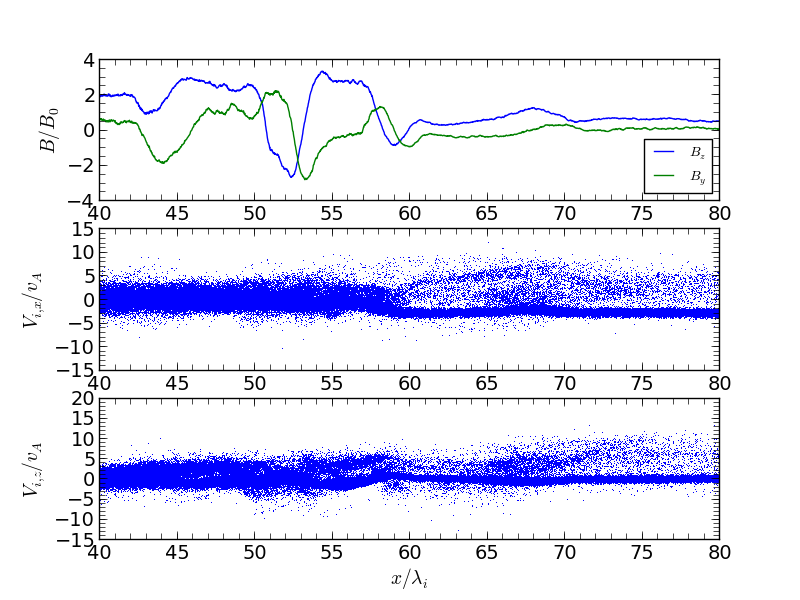
準平行衝撃波の構造(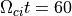 
)。¶
磁場の構造からは衝撃波面がどこにあるのか判断し難いが、イオンの分布関数から判断すると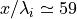 
付近が衝撃波面と考えて良いだろう。このように準平行衝撃波は準垂直衝撃波と比べて非常に複雑な構造をしている。他に顕著な特徴としては、上流へ流出する反射イオンの存在である。準垂直衝撃波では反射イオンは上流(foot)でジャイロ運動をした後に下流へと透過するが、準平行衝撃波では磁力線に沿ってイオンが衝撃波面から十分離れた位置まで到達している。
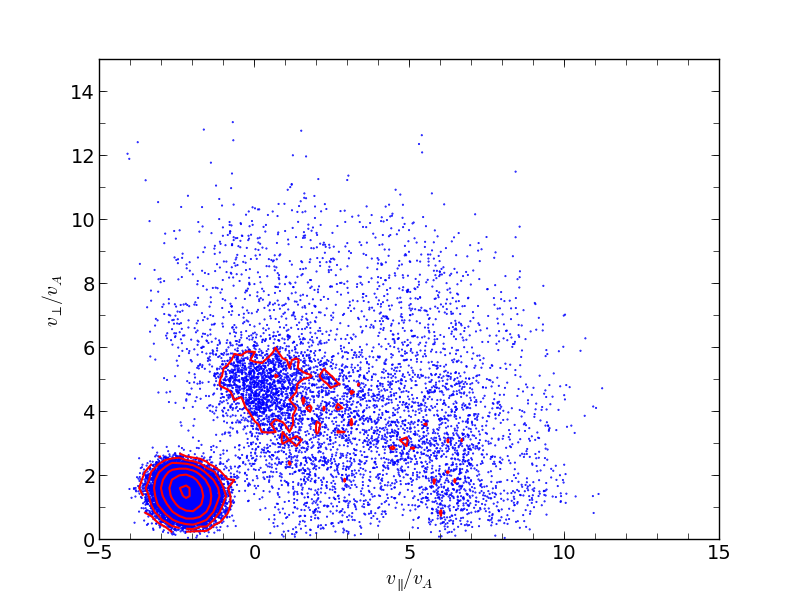
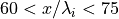の領域におけるイオンの速度分布関数。¶
上図には 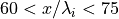の領域で積分したイオンの速度分布関数を示している。上流の冷たい成分と高エネルギーの成分が共存していることが見て取ることができ、高エネルギー成分は磁力線方向の速度成分だけでなく大きな垂直方向の速度成分を持つことも分かる。このような反射イオンはビーム不安定性を介して様々な波動を励起し得るが、典型的にはサイクロトロン共鳴によってAlfven波を励起する。励起されたAlfven波は反射イオンのピッチ角散乱を引き起こし、従って衝撃波近傍に高エネルギー粒子を閉じ込める役割を果たす。このような過程が1次Fermi加速機構のミクロなレベルにおける基本的な理解である。
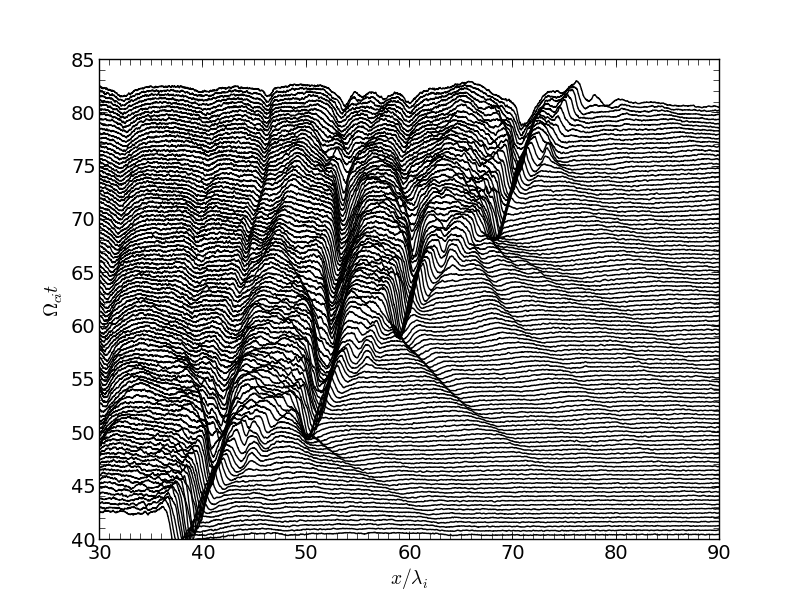
準平行衝撃波( 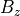)の時間発展。¶
準平行衝撃波のシミュレーションにおいても非定常性はしばしば観測される。上図に示すように、確かにこの例においても衝撃波構造の周期的な変動が見て取ることができる。この例では垂直衝撃波の場合と同様に衝撃波構造の再形成が起こっている。ただし時間・空間スケールは垂直衝撃波の場合に比べて非常に長くなっていることに注意されたい。
まとめ¶
ここでは主にイオンスケールに焦点を当てていたが、2000年頃からは衝撃波における電子スケールのダイナミクスを調べる研究が増えてきた。これは計算機の発達によりイオンと電子のスケールを分離したシミュレーションができるようになってきたからである。これによって非常にマッハ数の高い天体衝撃波における電子加速過程を調べたり、高時間分解能の直接観測との比較などが可能になってきた。その一方でイオンスケールの現象が完全に分かったわけでは無く、例えば上で見た非定常性の問題は依然として残されたままである。特に天体衝撃波のような高マッハ数の準平行衝撃波は多大な計算機資源を必要とすることから、これまでは粒子シミュレーションではあまり扱われて来なかったが、これは今後の面白い課題となるだろう。
