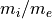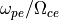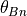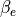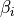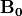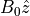無衝突衝撃波

著者:

松本洋介（千葉大学）

背景

1次元課題 で見たように、無衝突衝撃波の発展では様々なプラズマ不安定性が介在する。また、これら不安定性は衝撃波での散逸を担うだけでなく、非熱的粒子の生成にも重要な役割を果たす。衝撃波での粒子加速の標準理論として知られる衝撃波統計加速（1次Fermi加速）は、イオンに対する加速機構として重要であることが、地球磁気圏前面のバウショックにおける人工衛星のその場観測によって実証されてきた（ Scholer et al., 1980 ）。一方、熱的電子に対してはその適用が難しく、統計加速に至る前段階としての加速メカニズムが必要とされている（電子注入問題）。その有力な候補として、電子の衝撃波波乗り加速機構が挙げられる（ Shimada & Hoshino, 2000 ; McClements et al., 2001 ; Hoshino & Shimada, 2002 ）。反射イオンと上流電子の相互作用で励起されるBuneman不安定による強い静電場が電子を捉え、対流電場で加速するというものである。このような物理機構を理解する上で、PICシミュレーションは欠かせない研究手法であったが、計算機資源の制限から2000年代までは1次元計算による理解が主であった。しかし、2010年前後から２次元計算結果が報告されるようになり [1] 、多次元性による新たな特徴が明らかになりつつある（ Umeda et al., 2009 ; Amano & Hoshino, 2009 ; Lembege et al., 2009 ; Kato & Takabe, 2010b ; Riquelme & Spitkovsky, 2011 ; Matsumoto et al., 2012 ）。 しかし、依然2次元計算は大きな計算機リソースを必要とし、限られたパラメタ範囲で議論がされているため、電子加速メカニズムに対する多次元性の影響の理解は混沌としており、理解の整理があまり進んでいないのが現状である。 Matsumoto et al. (2012) は、PICシミュレーション資源を決めるイオン・電子質量比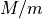（ M/m ）とアルヴェンマッハ数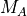（ M_A ）によって電子波乗り加速の効率がどのように変わるかを、単純な理論から導かれる関係式を元に調べた。

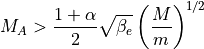
(1)M_A > \frac{1+\alpha}{2} \sqrt{\beta_e} \left(\frac{M}{m}\right)^{1/2}

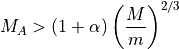
(2)M_A > (1+\alpha) \left(\frac{M}{m}\right)^{2/3}

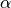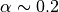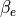ここで、 \alpha は反射イオンの上流密度に対する割合（高マッハ数衝撃波では \alpha \sim 0.2 程度）、 \beta_e は上流の電子プラズマベータを表す。式 (1) は衝撃波のフット領域におけるBuneman不安定の線形不安定条件を示し、式 (2) は電子を相対論的エネルギーまで加速するのに十分な強度の電場が励起されるための条件を示す。 上式をまとめた図 には、いくつかの電子ベータに対する式 (1) （破線）と式 (2) （実線）を、最近の2次元PICシミュレーションのパラメタと合わせてまとめてある。実線と破線ともに上のパラメタレンジの計算例では（図中Run AとRun C、ともに 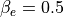\beta_e=0.5 ）、2次元計算においても電子が衝撃波波乗り加速によって効率的に電子が加速される様子が得られている。よって、現実的なイオン・電子質量比（1836）では、 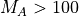M_A > 100 の条件が必要であり、このような条件が達成され得る超新星残骸衝撃波において重要な加速メカニズムであることが示唆される。しかし、高電子ベータ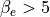（ \beta_e>5 ）の計算例（図中 Kato & Takabe 10 とRunD）では、上式を両方満たしていても非熱的電子が効率的に生成されず、上記理論が適用できない場合もあることに注意されたい。

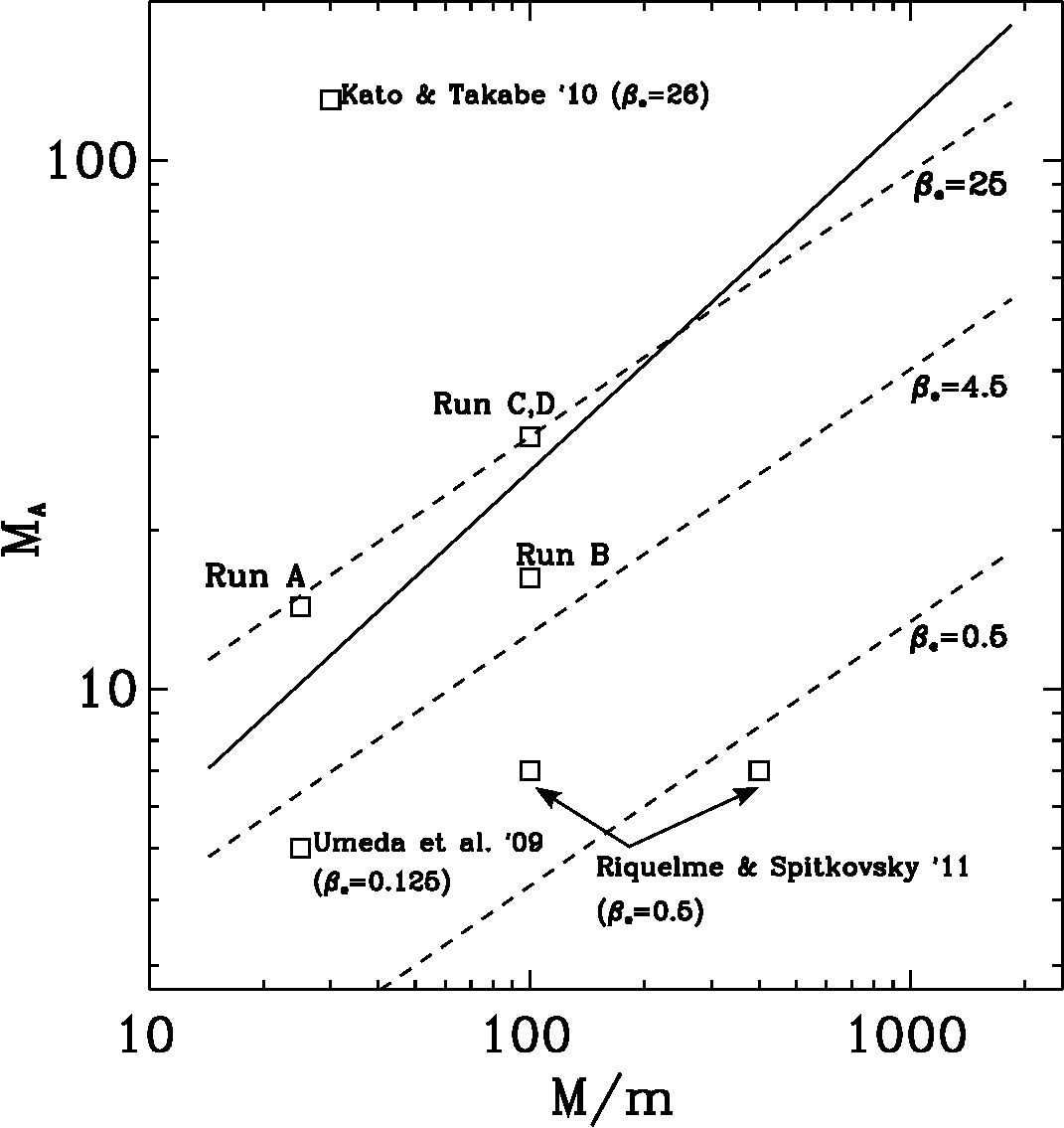
_images/sk2d_summary.png

式 (1) （破線）と式 (2) （実線）と、最近の2次元PICシミュレーションで使用されたパラメタとの関係（ Matsumoto et al., 2012 より）

一方で、実線と破線より下のパラメタ領域、つまり、比較的低いアルヴェンマッハ数の衝撃波では、Modified two-stream不安定が電子加速に重要になってくる（e.g., Scholer et al., 2003 ）。従って、地球磁気圏前面のバウショックなどで重要なメカニズムとなると考えられている。

Footnotes

課題設定

以下では、 Amano & Hoshino (2009) で使用されているパラメタでの計算例を示す。本パラメタは 上式をまとめた図 中のRunAに相当する。

m_i/m_e

25

\omega_{pe}/\Omega_{ce}

10

\theta_{Bn}

90

M_A

10.0

\beta_{e}

0.5

\beta_{i}

0.5

{\bf B_0}

B_0 \hat z

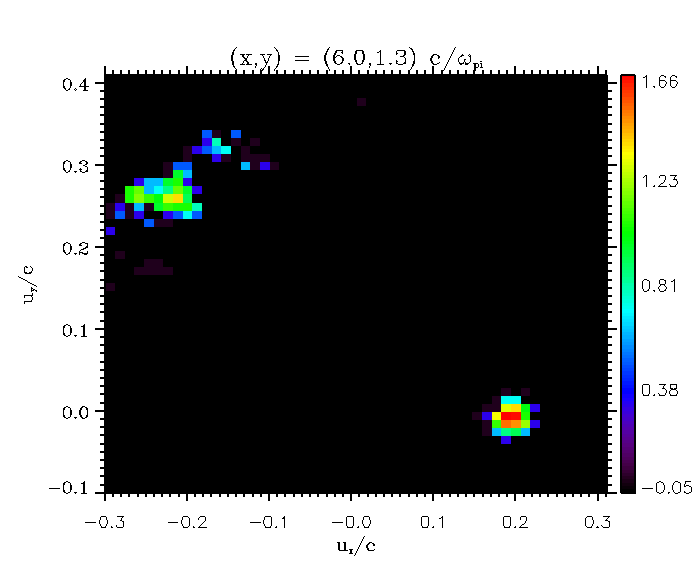
垂直衝撃波のうち、2次元計算では磁場を面内成分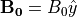（ {\bf B_0}=B_0 \hat y ）か、面外成分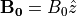（ {\bf B_0}=B_0 \hat z ）に設定する選択が可能である。ここでは、面外磁場のケースを取り扱う。

計算結果

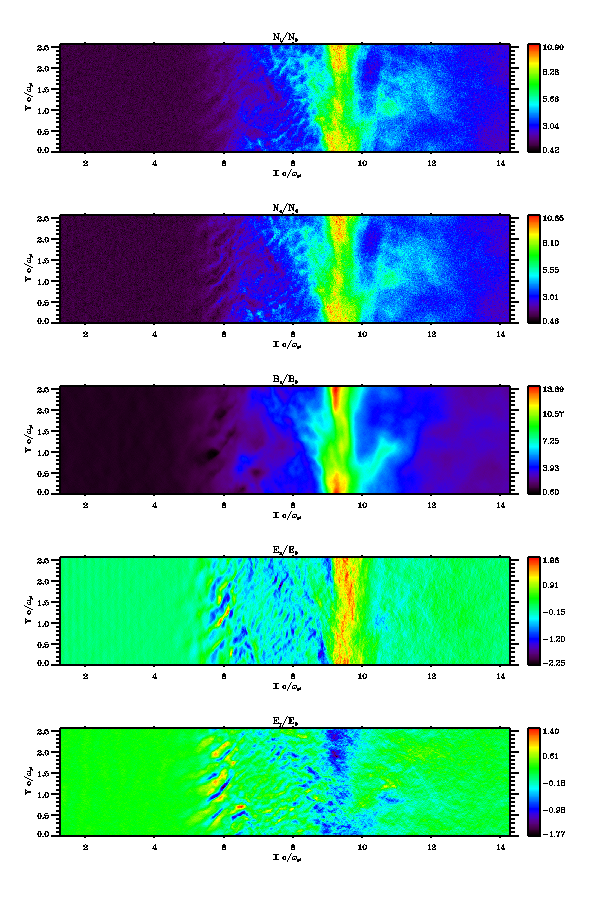
_images/sk2d_result.png

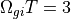\Omega_{gi}T=3 における2次元衝撃波計算結果。上から順に上流の密度で規格化したイオン、電子の密度、上流の磁場強度で規格化した磁場z成分、電場x成分、ｙ成分を表す。

pCANS の課題初期設定では、左手の境界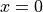（ x=0 ）が入射境界となっており、従って上流は左手になる。衝撃波面が 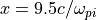x=9.5 c/\omega_{pi} 付近に見られ，強い磁場のピーク構造（overshoot）が見られる。また、その前方 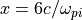x=6 c/\omega_{pi} 付近に電子スケールの強い電場構造が見られる。反射イオンの向き（-x, +y方向）に対応して、斜めの波面を持つ。この強い電場構造と相互作用しながら、電子は対流電場と逆方向（-y方向）に流れてエネルギーを得る。

_images/sk2d_psdi.png

衝撃波フット領域におけるイオンの分布関数。各ビン内の粒子の数をログスケールで描いている。

衝撃波フット先端での不安定性が励起されている領域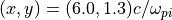（ (x,y) = (6.0,1.3) c/\omega_{pi} ）でのイオン分布関数を 分布関数図 に示す。上流の冷たい成分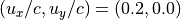（ (u_x/c,u_y/c)=(0.2,0.0) ）に加えて、上流に向かう反射イオンの成分が見られる。このような非等方的な分布関数が不安定性を励起する自由エネルギーとなる。

まとめ

以上では、 Amano & Hoshino (2009) のパラメタを例に取り、その2次元的構造を紹介した。さまざまな領域での電子のエネルギースペクトルを見ることで，その電子加速の様子がわかる。また、 上式をまとめた図 を参考にして、イオン・電子質量比とアルヴェンマッハ数を変えることにより、Buneman不安定の2次元的構造や電子の加速効率が変わることを確かめてみると良いであろう。また、同じ垂直衝撃波でも、面内磁場の場合には衝撃波面の構造が面外磁場のケースとは大きく変わることが、ハイブリッドシミュレーションで報告されている（ Burgess, 2006 ）。衝撃波面における電子加速もおもしろいテーマである。

参考文献