Weibel不安定¶
- 著者:
加藤恒彦(広島大学)
概要¶
プラズマが空間的に一様な場合でも、速度分布関数の形が熱平衡分布からずれているような場合には不安定性が発生しうる。これは、ミクロ不安定性あるいは運動論的不安定性と呼ばれるものである。特に、温度が非等方的なプラズマは不安定であり、背景磁場が無い場合に発生するこの種の不安定性はWeibel 不安定性と呼ばれる( Weibel, 1959 )。
2つの対向する粒子ビームがあるような場合も、速度分布が非等方的な状態であり、Weibel 不安定性と同様な不安定性が発生する( Fried, 1959 )。この場合は beam-Weibel 不安定性や filamentation 不安定性と呼ばれることも多い。線形成長段階では、不安定性の分散関係式は、ビーム速度に対応する実効的な温度を持つWeibel 不安定性の分散関係式と同じになる。
Weibel 不安定性は、電磁モード(横波モード)の不安定性であり、速度分散が大きい方向の電流密度の揺らぎが指数関数的に増大し、その方向に垂直な磁場成分も同時に成長する。不安定モードの位相速度はゼロの非伝播性の不安定性であり、静的な磁場がその場で成長していく。不安定性が非線形段階に入ると、電流密度分布は数多くの電流フィラメントに分裂する。そして、電流フィラメント自身が作る磁場で電流を運ぶ粒子が大きく曲げられるほど磁場が強くなるとサチュレーションし、磁場の成長は止まる( Kato, 2005 )。サチュレーション後は、電流フィラメント同士が合体していきながら進化し、それに伴って磁場はゆっくりと減衰していく。
宇宙空間でも、このような不安定性は様々な現象に付随して発生すると考えられている。たとえば、ガンマ線バーストに関係した相対論的衝撃波の下流で粒子の速度分布が非等方的になり、それにより Weibel 不安定性が発生して非常に強い磁場を作るモデルなどが考えられている( Medvedev & Loeb, 1999 )。また、近年のPICシミュレーションにより、背景磁場が無いプラズマ中でも、Weibel 不安定性により作られる非常に強い磁場が散逸の役割を果たす無衝突衝撃波が形成されることが示されている( Kato, 2007 ; Spitkovsky, 2008 )。さらには、磁気リコネクションのアウトフロージェットでも Weibel 不安定性によって乱流磁場が作られる( Zenitani & Hesse, 2008 ; Swisdak et al. 2008 )。このように、宇宙空間でも激しいプラズマの衝突が起きるような場合には、それに伴ってWeibel不安定性が発生することが考えられる。
線形理論¶
今、複数の種類の粒子からなるプラズマを考え、それぞれ、  方向の温度 (
方向の温度 ( 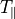 ) が
) が 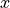 ,
, 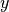 方向の温度 (
方向の温度 ( 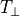 ) と異なる場合を考える。粒子種
) と異なる場合を考える。粒子種  の温度比を
の温度比を 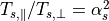 と書き、
と書き、  軸に垂直な方向の熱速度を
軸に垂直な方向の熱速度を 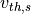 とすると、分布関数
とすると、分布関数 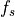 は以下のように与えられる。
は以下のように与えられる。
(1)¶![f_s(v_x, v_y, v_z) = \frac{n_s}{\pi^{3/2} \alpha_s v_{th,s}^3}\exp\left[ -\frac{v_x^2+v_y^2}{v_{th,s}^2} -\frac{v_z^2}{\alpha_s^2 v_{th,s}^2} \right]](_images/math/9689be7bd7b9e47cac705d523527087ad2b36f47.png)
ここで 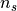 は数密度である。
は数密度である。
背景磁場が無い場合の、  軸に垂直な方向に波数ベクトルを持つ電磁モード(横波モード)の分散関係式は、以下のように与えられる(
軸に垂直な方向に波数ベクトルを持つ電磁モード(横波モード)の分散関係式は、以下のように与えられる( 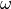 がモードの振動数、
がモードの振動数、 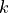 が波数であり、
が波数であり、 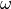 は一般に複素数である)。
は一般に複素数である)。
(2)¶![\omega^2 - (kc)^2 + \sum_s \omega_{ps}^2 \left[ A_s + (A_s+1) \zeta_s Z(\zeta_s) \right] = 0](_images/math/509c6e5fea8093139ead665cb81df6dc726f45a0.png)
ここで
(3)¶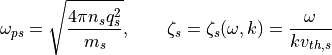
であり、 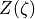 はプラズマ分散関数
はプラズマ分散関数
(4)¶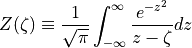
である。 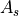 は温度の非等方性の大きさを表すパラメータ
は温度の非等方性の大きさを表すパラメータ
(5)¶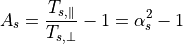
で、等方的な場合に 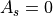 となる。
となる。
分散関係式 (2) は、ある条件下で不安定解 ( 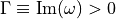 ) を持つ。これが Weibel 不安定性と呼ばれる不安定モードである。不安定になる波数の最大値
) を持つ。これが Weibel 不安定性と呼ばれる不安定モードである。不安定になる波数の最大値  は、式 (2) から
は、式 (2) から
(6)¶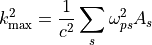
と求められる。これから、特に不安定条件は、 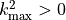 すなわち
すなわち
(7)¶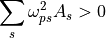
で与えられることがわかる。
非等方性があまり大きくなく、  が成り立つ場合には、成長率は
が成り立つ場合には、成長率は 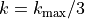 で最大値
で最大値
(8)¶![\Gamma_\mathrm{max} =
\frac{2}{9} \sqrt{\frac{3}{\pi}} k_\mathrm{max}^3 c^2 \left[ \sum_s \omega_{ps}^2 (A_s+1)/v_{th,s} \right]^{-1}](_images/math/3355dec07457c2b687d7e8b871f749f63b897ae5.png)
を取る。
例として、電子・陽電子プラズマ中のWeibel不安定性の成長率を 図 に示す。ここで、成長率は電子プラズマ振動数 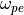 で規格化している。いくつかの非等方性
で規格化している。いくつかの非等方性 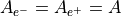 の値に対して成長率をプロットしている。(ここでは垂直方向の熱速度は
の値に対して成長率をプロットしている。(ここでは垂直方向の熱速度は 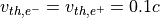 に固定し、
に固定し、  方向の熱速度を変化させている。)温度非等方性が大きくなるほど、より大きな波数(より短い波長)まで不安定になり、最大成長率も大きくなることがわかる。
方向の熱速度を変化させている。)温度非等方性が大きくなるほど、より大きな波数(より短い波長)まで不安定になり、最大成長率も大きくなることがわかる。
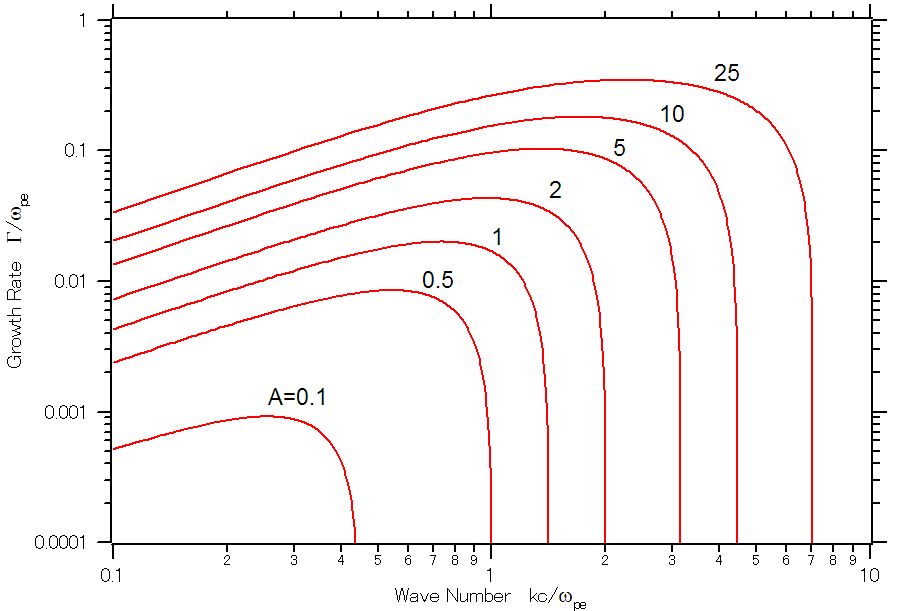
電子・陽電子プラズマ中のWeibel不安定性の線形成長率。縦軸は電子プラズマ振動数 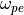 で規格化した成長率、横軸は
で規格化した成長率、横軸は 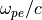 で規格化した波数である。温度非等方性(
で規格化した波数である。温度非等方性( 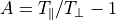 )が
)が 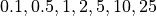 の場合を示す。¶
の場合を示す。¶
対向ビームの場合など、温度が等方的でもドリフト速度を持つような場合の分散関係式は、実効的な非等方性を
(9)¶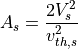
とした場合の分散関係式 (2) と等しくなる(e.g., Kato & Takabe, 2010a )。したがって、このような場合でも Weibel 不安定性と同様な不安定性が起きる。
シミュレーション結果¶
2次元のPICシミュレーションにょり、この不安定性をシミュレーションしてみよう。上の例と同様に、ここでは背景磁場の無い温度非等方な電子・陽電子プラズマ中のWeibel不安定性を考える。シミュレーション平面を  平面とし、
平面とし、 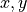 方向の温度に比べて
方向の温度に比べて  方向の温度が高いとする。以下では、
方向の温度が高いとする。以下では、 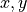 方向の熱速度は
方向の熱速度は 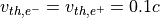 とし、
とし、  方向の熱速度はこの5倍とする(
方向の熱速度はこの5倍とする( 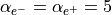 )。従って、非等方性パラメータは
)。従って、非等方性パラメータは 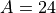 の場合である。
の場合である。
線形理論によると、 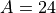 の場合の最も不安定な波長は
の場合の最も不安定な波長は 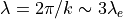 である( 図 の
である( 図 の 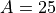 の場合を参照)。ここで、
の場合を参照)。ここで、 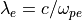 は電子 skin depth と呼ばれる長さである。この波長
は電子 skin depth と呼ばれる長さである。この波長 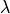 を6、7個含むように、系のサイズは
を6、7個含むように、系のサイズは 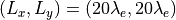 とする。グリッド数は
とする。グリッド数は 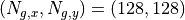 とし、グリッドあたりの粒子数は
とし、グリッドあたりの粒子数は 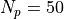 個とする。初期状態では、電場も磁場もゼロとする。境界条件は、粒子も電磁場も周期境界条件を用いる。
個とする。初期状態では、電場も磁場もゼロとする。境界条件は、粒子も電磁場も周期境界条件を用いる。
実際の pCANS を用いた計算では、 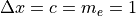 とした単位が用いられる。これとグリッド数
とした単位が用いられる。これとグリッド数 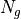 およびグリッドあたりの粒子数
およびグリッドあたりの粒子数 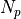 から、この単位での主な物理量の値が以下のようにして求められる。まず、電子 skin depth
から、この単位での主な物理量の値が以下のようにして求められる。まず、電子 skin depth 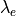 は、系のサイズについての条件から
は、系のサイズについての条件から
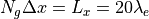
を満たしている必要がある。これから
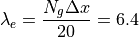
を得る。これを用いると電子プラズマ振動数は
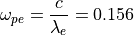
となり、電子と陽電子の電荷の大きさ  は
は
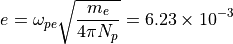
のように求められる。
シミュレーションの結果得られたエネルギーの進化を 図 に示す。磁場のエネルギーはWeibel不安定性によって 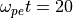 ぐらいまでは指数関数的に成長し、その後サチュレーションしているのがわかる。この 図 から読み取れる成長率は
ぐらいまでは指数関数的に成長し、その後サチュレーションしているのがわかる。この 図 から読み取れる成長率は 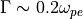 であり、 成長率の図 の
であり、 成長率の図 の 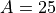 の場合の最大成長率とほぼ一致している。サチュレーション時には、磁場エネルギーは全エネルギーの約1割にも達し、非常に強い磁場が作られていることがわかる。その一方で、粒子のエネルギーはその分だけ減少している。サチュレーション後には、磁場エネルギーはゆっくりと減衰していく。
の場合の最大成長率とほぼ一致している。サチュレーション時には、磁場エネルギーは全エネルギーの約1割にも達し、非常に強い磁場が作られていることがわかる。その一方で、粒子のエネルギーはその分だけ減少している。サチュレーション後には、磁場エネルギーはゆっくりと減衰していく。
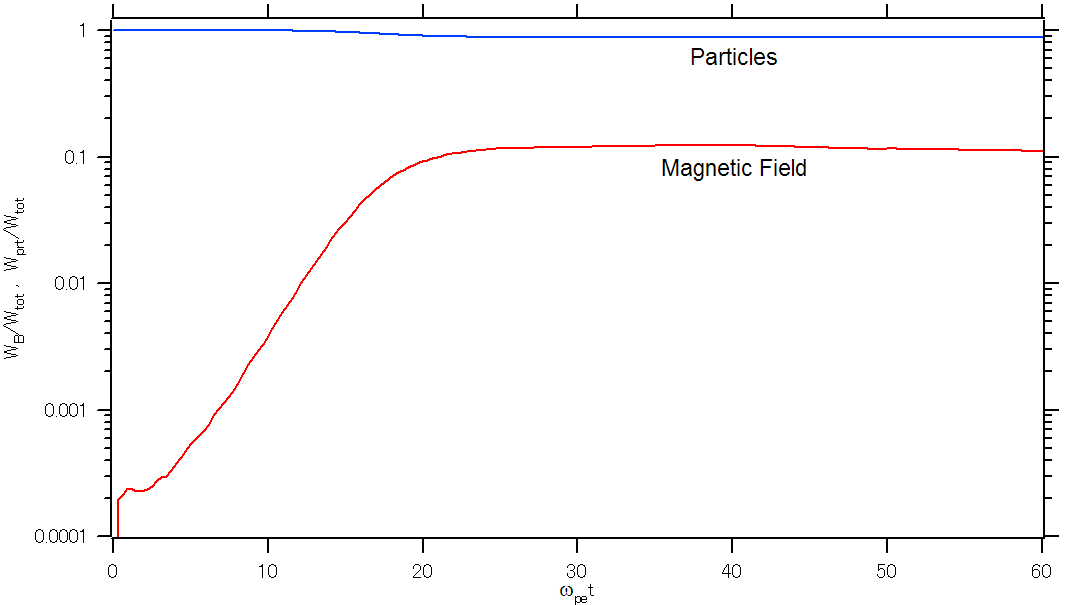
系全体のエネルギーで規格化した磁場と粒子のエネルギーの時間進化(赤:磁場のエネルギー、青:粒子のエネルギー)。¶
図 に電流密度の  方向成分(
方向成分( 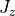 )の時間進化を示す。
)の時間進化を示す。 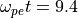 では、ほぼ線形理論で予想される波長で
では、ほぼ線形理論で予想される波長で 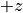 ,
, 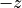 両方向の電流が成長しつつあり、サチュレーション時刻付近の
両方向の電流が成長しつつあり、サチュレーション時刻付近の 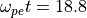 では、その波長スケールの数多くの電流フィラメントが形成されているのがわかる。さらに時間が経過すると、電流フィラメントのスケールは大きくなる。これは、電流フィラメント同士の合体によるものである。合体に伴い、電流密度自体の値は減少していく。
では、その波長スケールの数多くの電流フィラメントが形成されているのがわかる。さらに時間が経過すると、電流フィラメントのスケールは大きくなる。これは、電流フィラメント同士の合体によるものである。合体に伴い、電流密度自体の値は減少していく。
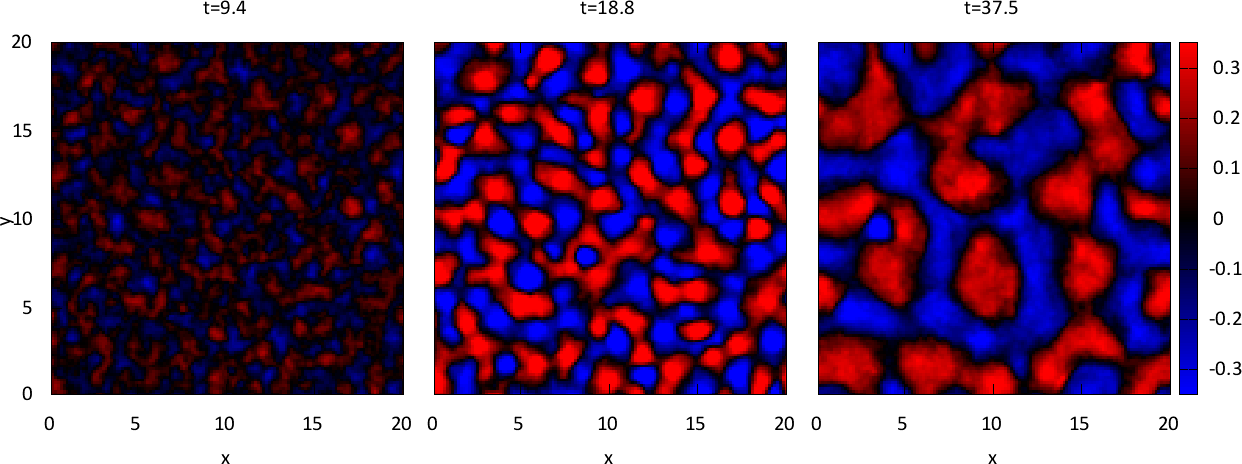
 方向の電流密度 (
方向の電流密度 ( 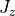 ) の時間進化。横軸、縦軸はそれぞれ電子 skin depth (
) の時間進化。横軸、縦軸はそれぞれ電子 skin depth ( 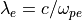 )で規格化した
)で規格化した 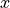 座標と
座標と 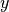 座標であり、時刻は左から順に
座標であり、時刻は左から順に 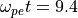 ,
, 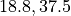 となっている。¶
となっている。¶
同様に、磁場の大きさ (  )の時間進化を 図 に示す。アンペールの法則に従って、
)の時間進化を 図 に示す。アンペールの法則に従って、 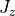 の空間分布に対応して磁場が作られていることがわかる。電流が強くなれば磁場も強くなり、電流フィラメントのスケールが合体により大きくなれば、それに対応して磁場のスケールも大きくなる。
の空間分布に対応して磁場が作られていることがわかる。電流が強くなれば磁場も強くなり、電流フィラメントのスケールが合体により大きくなれば、それに対応して磁場のスケールも大きくなる。
磁場の大きさ (  ) の時間進化。¶
) の時間進化。¶
不安定性のサチュレーションは、自分自身が作る磁場により電流を運ぶ荷電粒子の軌道が大きく曲げられ、それ以上電流が運べなくなることにより起きる。実際、サチュレーション付近の時刻  では、
では、  方向の典型的な速度
方向の典型的な速度  を持つ粒子のジャイロ半径は
を持つ粒子のジャイロ半径は 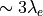 程度であり、電流フィラメントのサイズとほぼ同じスケールになっていることがわかる。
程度であり、電流フィラメントのサイズとほぼ同じスケールになっていることがわかる。
このような1つの円柱状の電流フィラメントが運べる全電流には、上限があることが知られており、Alfv'enの臨界電流と呼ばれる( Alfven, 1939 )。この電流の上限値 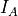 は、粒子の速度
は、粒子の速度  (および、それにより決まるローレンツ因子
(および、それにより決まるローレンツ因子 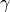 )のみに依存し、フィラメントの半径には依存しない。
)のみに依存し、フィラメントの半径には依存しない。
(10)¶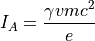
このため、サチュレーション後は、電流フィラメントは電流を 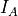 に保ったまま合体し、より大きなスケールへ進化していく。この際、フィラメント内の電流密度は減少するので、平均的な磁場の強度は減少していく。
に保ったまま合体し、より大きなスケールへ進化していく。この際、フィラメント内の電流密度は減少するので、平均的な磁場の強度は減少していく。
まとめ¶
背景磁場の無い温度非等方なプラズマ中には Weibel 不安定性が発生する。不安定性に伴い、電流密度の揺らぎと磁場が成長していく。非線形段階では、多数の電流フィラメントが形成され、フィラメントが作る磁場により電流を運ぶ粒子の軌道が大きく曲げられるようになると不安定性の成長は止まる。その後は、フィラメント同士が合体していくことで、長波長へ進化していく。
ここでは、電子・陽電子プラズマの場合に、実際にWeibel不安定性のシミュレーションを行い、線形段階の成長から、非線形段階での電流フィラメントの形成、サチュレーション、そして、その後の電流フィラメント同士の合体による長波長への進化を見てきた。組成が電子・陽子の場合、速度が相対論的な場合、対向ビームがある場合、などに対しても、PICシミュレーションを用いて同様に調べていくことができる。
