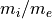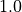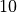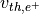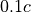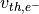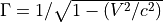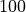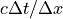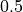数値チェレンコフ不安定¶
- 著者:
池谷直樹、松本洋介 (千葉大学)、加藤恒彦(広島大学)
概要¶
PICシミュレーション法において光速に近い相対論的な速度を持つプラズマを扱う際に、数値チェレンコフ放射( Godfrey et al., 1974 )と呼ばれる数値的な不安定性が発生することが知られている。これは、PIC法の特徴である電磁波の差分解法に基づいた現象である。PIC法において電磁波はシミュレーション空間内に定義されたグリッド点において入れ子状に配置され、その格子間隔や時間ステップは有限な値を持つ。そのため、差分近似による数値分散が発生し、ナイキスト波数近くになるにつれ電磁波は光速を下回る。そこに相対論的なプラズマを流した際に、プラズマの流れが電磁波を追い越し、数値チェレンコフ放射による数値的な不安定性が発生する。この数値チェレンコフ放射の不安定性により発生する電場、磁場のエネルギーは、系の全エネルギーの約10%に達し、粒子の運動に対して影響を与えると考えられる。そのため、無衝突衝撃波における粒子加速の解析( Spitkovsky,2008 )など、非熱的な粒子を扱う際には無視できない重要な問題となってくる。本課題では、PIC法における差分解法に伴う電磁波の分散関係式を示し、相対論的なプラズマとの関係を求めた上で、実際に相対論的な速度を持つ系における2次元PICシミュレーションを行い、その結果と比較する。この数値チェレンコフ放射は、差分近似による電磁波の数値分散など、PIC法の基本的な現象に基づいたものであるため、本課題の内容を理解しておくことは、PIC法による他の様々な解析において手助けとなるであろう。
電磁波の数値分散関係¶
PICシミュレーションで解くマクスウェル方程式は
(1)¶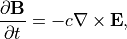
(2)¶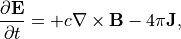
である。PIC法において電磁波は 電磁波の配置図 のように、シミュレーション空間内に定義されたグリット点に配置される。電磁波の標準解法として知られるFDTD法では、式 (1) , (2) は2次元 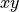 平面において
平面において
(3)¶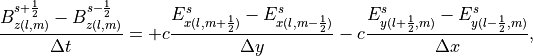
(4)¶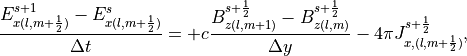
(5)¶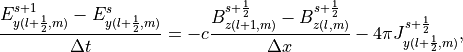
のように差分化される。ここで、 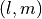 はそれぞれグリッド点の
はそれぞれグリッド点の 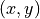 成分の座標を表し、
成分の座標を表し、  はタイムステップを表す。式 (3) - (5) に離散化させた平面波の式
はタイムステップを表す。式 (3) - (5) に離散化させた平面波の式
(6)¶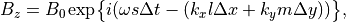
(7)¶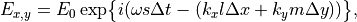
を代入することで、FDTD法における電磁波の分散関係式は
(8)¶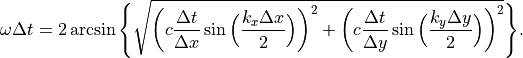
と与えられる。 pCANS では電磁波の差分解法として、上記のFDTD法と異なる陰的解法を採用している( 電磁波の数値解法 を参照のこと)。陰的解法においては、式 (3) - (5) とタイムステップの異なる形で
(9)¶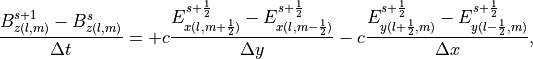
(10)¶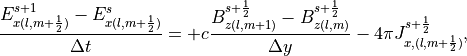
(11)¶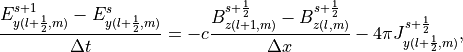
のように差分化し、各式右辺のタイムステップ 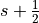 における物理量を
における物理量を
(12)¶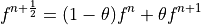
として与える。その後、離散化させた平面波の式 (6) , (7) を代入することにより、 の陰的解法における電磁波の分散関係式の実部・虚部はそれぞれ、
(13)¶![\Re\bigl[\omega\Delta t\bigr]=2\arctan\Biggl[
\frac{1}{4}\frac
{\sqrt{\frac{1}{
(c\frac{\Delta t}{\Delta x}\sin{\frac{k_x\Delta x}{2}})^2+(c\frac{\Delta t}{\Delta y}\sin{\frac{k_y\Delta y}{2}})^2}}}
{(\theta-\frac{1}{2})^2+\frac{1}{4}{\frac{1}{(c\frac{\Delta t}{\Delta x}\sin{\frac{k_x\Delta x}{2}})^2+(c\frac{\Delta t}{\Delta y}\sin{\frac{k_y\Delta y}{2}})^2}}}
\Biggr]](_images/math/cb625cd0f2529ecc46153a7b4ca914dd94a0580f.png)
(14)¶![\Im\bigl[\omega\Delta t\bigr]=2\arctan\Biggl[
\frac{1}{2}\frac
{(\theta - \frac{1}{2})}
{(\theta-\frac{1}{2})^2+\frac{1}{4}{\frac{1}{
(c\frac{\Delta t}{\Delta x}\sin{\frac{k_x\Delta x}{2}})^2+(c\frac{\Delta t}{\Delta y}\sin{\frac{k_y\Delta y}{2}})^2}}}
\Biggr]](_images/math/4d18b3f8c876d688647bd7ef5807a3c37c9051c2.png)
となる。陰的解法の特徴として現れる 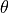 は
は 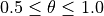 の値をとり、シミュレーションの際には
の値をとり、シミュレーションの際には 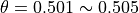 で与えるため、ここでは簡単に
で与えるため、ここでは簡単に 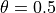 をとると、陰的解法における電磁波の数値分散関係式は実部のみとなり
をとると、陰的解法における電磁波の数値分散関係式は実部のみとなり
(15)¶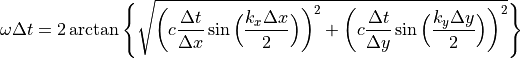
として与えられる。

電磁波の数値分散関係の図¶
電磁波の数値分散関係の図 は、式 (15) を波数空間上でプロットしたものであり、ナイキスト波数 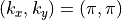 に近づくにつれて数値分散を起こし、位相速度が光速を下回ることが確認できる。
に近づくにつれて数値分散を起こし、位相速度が光速を下回ることが確認できる。
課題設定¶
以下では、相対論的なプラズマを用いた2次元のPICシミュレーションにより、数値チェレンコフ放射による不安定性を確認する。シミュレーション空間の設定は、シミュレーション平面をx-y平面とし、電子慣性長 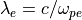 に対して系のサイズを
に対して系のサイズを 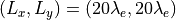 とする。グリッド数は
とする。グリッド数は 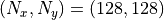 とし、初期状態において電場、磁場は無いものとする。この空間中に
とし、初期状態において電場、磁場は無いものとする。この空間中に  方向に相対論的な速度
方向に相対論的な速度 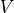 を持つ陽電子・電子プラズマを
を持つ陽電子・電子プラズマを 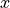 方向に流す。境界条件は電磁波、粒子どちらも周期境界条件を用いる。本課題で用いるパラメータの基本例は以下に示す。
方向に流す。境界条件は電磁波、粒子どちらも周期境界条件を用いる。本課題で用いるパラメータの基本例は以下に示す。
CFL number =
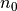 は、初期のセルあたりの粒子数であり,
は、初期のセルあたりの粒子数であり, 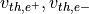 はそれぞれ、陽電子、電子の熱速度を表す。また、
はそれぞれ、陽電子、電子の熱速度を表す。また、 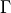 はバルク速度
はバルク速度 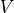 のローレンツ因子である。
のローレンツ因子である。
シミュレーション結果¶
pCANS の2次元コードを用いて1次元方向に相対論的な速度を持ったプラズマを流した際、陰的解法における電磁波の分散関係式とプラズマの流れ(エントロピーモード)の分散関係の関係は下図のように表される。

緑:電磁波の数値分散関係、青: 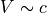 で流れるプラズマの分散関係(エントロピーモード)¶
で流れるプラズマの分散関係(エントロピーモード)¶
図 から、プラズマが流れる速度が電磁波を越える部分が現れることが確認できる。この線は 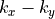 の波数空間上において
の波数空間上において
(16)¶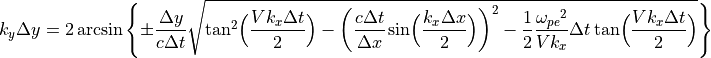
と求めることができ、この理論線上において数値チェレンコフ放射が発生し、不安定性の成長が起こると考えられる。
注釈
プラズマの速度が 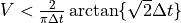 (上記パラメタの場合
(上記パラメタの場合 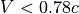 )であるような条件下では、ナイキスト波数
)であるような条件下では、ナイキスト波数 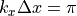 においてプラズマの流れの分散関係が折り返される、エイリアスと電磁波の分散関係との交差による数値チェレンコフ不安定性も重要になり( Godfrey & Vay, 2013 ; Vay et al., 2013 )、式 (16) と異なる形で発生する。しかし、本課題のような光速に近い相対論的なプラズマ
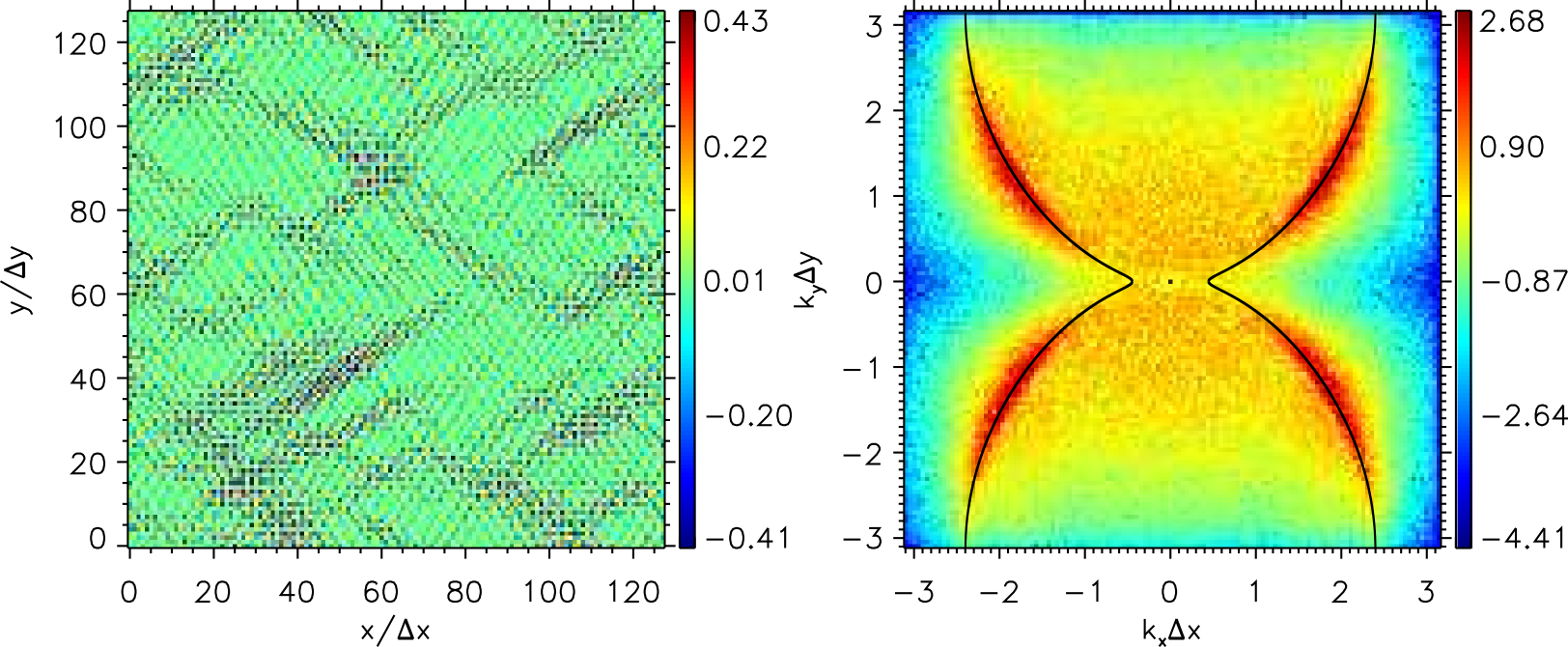
においてプラズマの流れの分散関係が折り返される、エイリアスと電磁波の分散関係との交差による数値チェレンコフ不安定性も重要になり( Godfrey & Vay, 2013 ; Vay et al., 2013 )、式 (16) と異なる形で発生する。しかし、本課題のような光速に近い相対論的なプラズマ 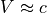 を用いたシミュレーションにおいては、差分法に基づく pCANS ではエイリアスによる影響は小さい。
を用いたシミュレーションにおいては、差分法に基づく pCANS ではエイリアスによる影響は小さい。
以下では、初期の課題設定におけるシミュレーション結果を示す。
 における磁場
における磁場 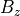 を、左図は実空間、右図はフーリエ空間で表したもの。カラー値は粒子のエネルギーで規格化。¶
を、左図は実空間、右図はフーリエ空間で表したもの。カラー値は粒子のエネルギーで規格化。¶
右図のフーリエ空間上での磁場 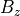 のカラー図において、重ねてプロットした黒線は式 (16) を表したものであり、確かに式 (16) で表した理論線上において、数値チェレンコフ放射の不安定性が発生することが確認できた。
のカラー図において、重ねてプロットした黒線は式 (16) を表したものであり、確かに式 (16) で表した理論線上において、数値チェレンコフ放射の不安定性が発生することが確認できた。
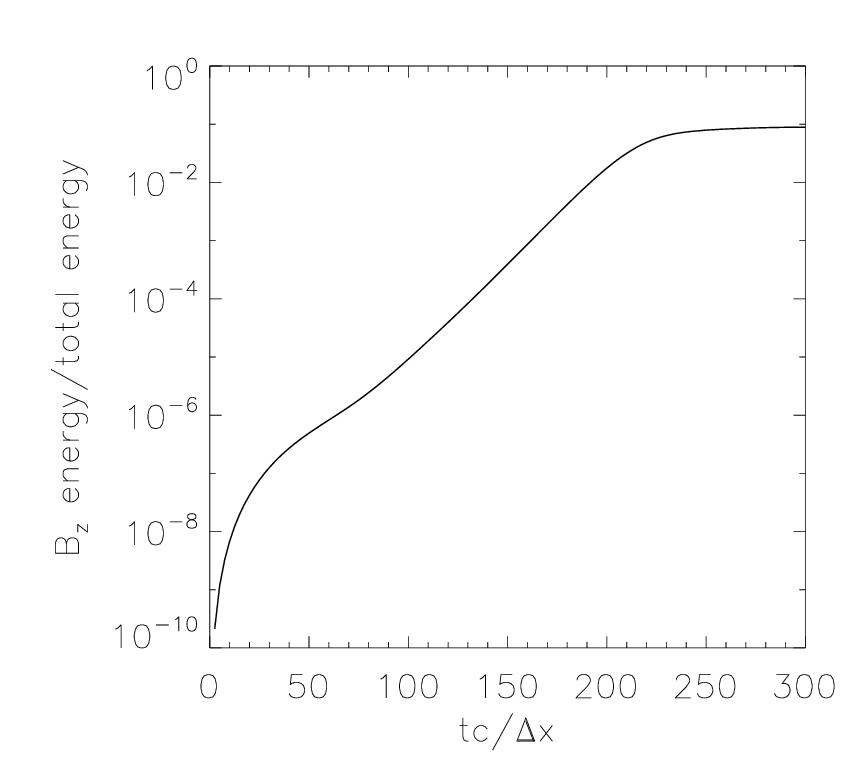
磁気エネルギーの時間発展図。 縦軸は 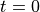 における全エネルギー(運動エネルギー)で、横軸は
における全エネルギー(運動エネルギー)で、横軸は 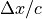 でそれぞれ規格化。¶
でそれぞれ規格化。¶
図 は磁場エネルギーの時間変化を表す。数値チェレンコフによる磁場のエネルギー増加は全エネルギーの10%にも達するため、相対論的流れ場における粒子加速問題など取り扱う際に問題となる。
まとめ¶
本課題では、 pCANS の相対論的プラズマを用いた2次元シミュレーションにより数値チェレンコフ放射による不安定性を確認した。また、その結果が電磁波の分散関係から求めた数値チェレンコフ放射が発生する理論線と一致することも確認できた。本課題とは環境設定が異なる無衝突衝撃波のシミュレーションにおいても、流入させる粒子の速度を光速に近い相対論的な速度にすることで、数値チェレンコフ不安定は確認できるであろう。このような数値チェレンコフ放射によって発生する電場や磁場の不安定性は、粒子に影響を及ぼすほどの大きさであるため、相対論的無衝突衝撃波における粒子加速の解析などの相対論的な系を扱う多次元PICシミュレーションにおいては、重要な問題として知られている。この問題に対しては、長年、様々な手法による対処がなされてきた。一つは、フーリエ空間でマクスウェル方程式を解くことによって、数値分散の起こらない解析解を得るPSATD法がある( Vay et al., 2013 )。また、近年では差分解法の形を保ったまま数値チェレンコフによる不安定性を抑制する手法も報告されている( Godfrey & Vay, 2013 ; Xu et al., 2013 )。本課題の内容からこれらの手法を理解するのは容易ではないが、古くからある数値チェレンコフ放射という現象が、近年に到るまで様々な研究がなされていることがわかる。