IDLによる解析・可視化

著者:

松本洋介（千葉大学）、簑島敬（JAMSTEC）

本章では、 pCANS での解析・可視化ツールであるIDL（Interactive Data Language）の基本的な使い方と、用意されているIDLプロシージャ及びアニメーションの作り方を説明します。IDLのバージョンが8.0以降では、グラフィックス環境が大きく変わり、可視化が容易かつ洗練されました。さらなる詳細は IDLのドキュメントサイト を参照してください。

$PCANS_DIR/idl"内には、以下のようなIDLのプロシージャが用意されています。これらは各課題から共通して使えるものです。

課題に固有のプロシージャは各課題ディレクトリ内に用意されており、共通プロシージャを内部で利用しています。例えば、"$PCANS_DIR/em1d/md_wave/batch.pro"と"$PCANS_DIR/em1d/md_whistler/batch.pro"にサンプルプロシージャがあります。

環境変数の設定

環境変数$IDL_STARTUPに$PCANS_DIR/idl/init.proを設定します。

bashの場合、

export IDL_STARTUP = $PCANS_DIR/idl/init.pro

tcshの場合、

setenv IDL_STARTUP $PCANS_DIR/idl/init.pro

$PCANS_DIR/idl/init.pro内には、pathの設定、IDL内の環境の設定等が含まれており、IDL起動時に自動的に設定されます。各自の好みに合わせて修正してください。

データの読み込み

ASCIIデータを読み込む共通プロシージャが用意されています。

file_read.pro

Name
  file_read
  ASCIIデータを読み込む

Syntax
  result= file_read([filename][,format=format][,/string]
                    [,/silent][,/compress])

Arguments
  filename
    読み込むデータのファイル名。ワイルドカードが使え、パターンに
    マッチしたファイルを一度に読み込む。ただし、読みこむ全ての数
    値データ配列数は等しい必要がある。

Keywords
  format
    読み込むデータのデータフォーマットを指定する。

  string
    読み込むデータを文字列として読み込む。

  silent
    読み込むデータ情報の出力をしない。

  compress
    圧縮されたデータを読み込む

Example1
  IDL> data= file_read('010000_bx.dat')

Example2
  IDL> dataset = file_read('010000_*.dat')

1次元プロット

1次元のプロットを作成する方法を以下に簡単に示します。

IDL> data=file_read('030000_*.dat') ;; データの読み込み
IDL> xax = findgen(2047)
IDL> pl1=plot(xax,data[*,8],xtitle='$x$',ytitle='$B_z$') ;; Latexのコマンドが使える！

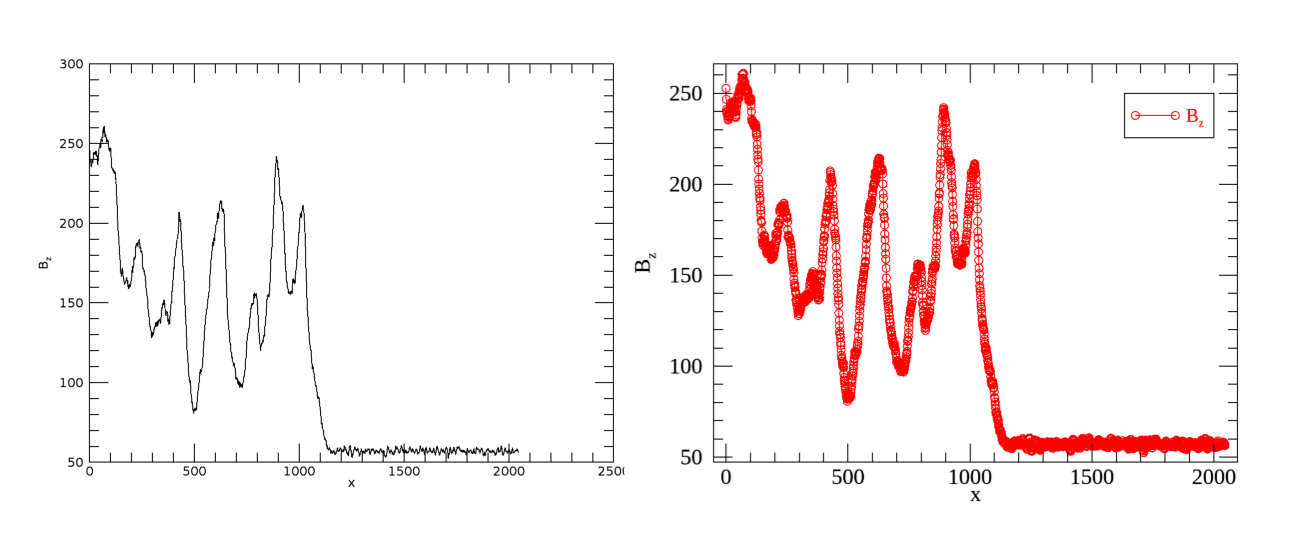
1次元プロットの例。左は修正前、右は後から修正を加えたもの。

これに修正を加える場合は、plのpropertyに値を代入します。

IDL> pl1.symbol='circle' ;; ○の追加
IDL> pl1.color='red'     ;; 線を赤に
IDL> pl1.xstyle=3        ;; x方向の描画範囲を少し広げる
IDL> pl1.ystyle=3        ;; y方向の描画範囲を少し広げる
IDL> pl1.font_size=16    ;; フォントサイズを16に
IDL> pl1.font_name='Times' ;; フォントをTimesに
IDL> leg=legend(target=pl1,position=[2000,250],/data,/auto_text_color)
IDL> leg.font_name = 'Times'
IDL> leg.font_size = '14'
IDL> leg.label = '$B_z$'

のようににして後からプロットの属性に変更を加えることができます。GUIでの操作も可能です。凡例を加えるには、legend関数を使います。

複数のプロットを並べて表示する場合はlayoutオプションを使います。この例では2x2のパネル状に並べて表示します。

IDL> pl1=plot(x,data[*,8],xstyle=1,ystyle=2,color='red',$
IDL>          layout=[2,2,1])
IDL> pl2=plot(x,data[*,10],xstyle=1,ystyle=2,color='blue',$
IDL>          layout=[2,2,2],/current)
IDL> pl3=plot(x,data[*,11],xstyle=1,ystyle=2,color='purple',$
IDL>          layout=[2,2,3],/current)
IDL> pl4=plot(x,data[*,15],xstyle=1,ystyle=2,color='green',$
IDL>          layout=[2,2,4],/current)
IDL> pl1.title='$B_z$'
IDL> pl2.title='$N_i$'
IDL> pl3.title='$E_x$'
IDL> pl4.title='$V_{xi}$'

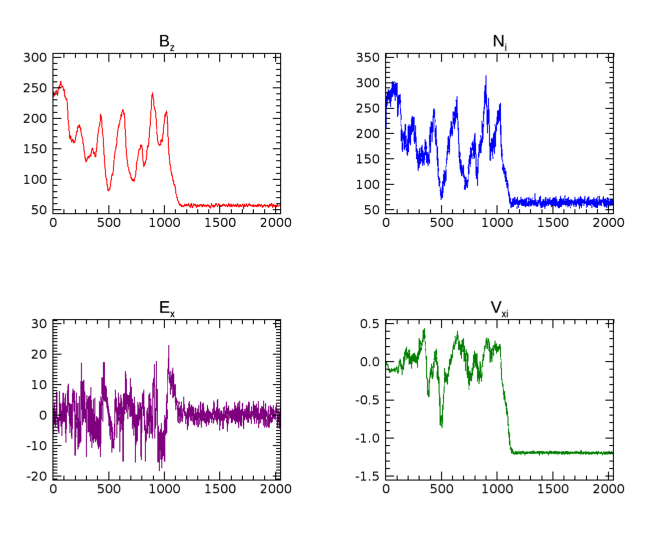
上記の設定の結果

するとこのように表示されます。

その他の応用は、サンプルプロシージャ $PCANS_DIR/em1d/md_shock/batch.proをご覧ください。また、plot, legend関数に関する情報は

IDL> ?plot
IDL> ?legend

とすることで、ブラウザで見ることができます。

2次元可視化

カラーマップ図

物理量の２次元プロファイルを表示する方法を以下に示します。

IDL> data = file_read('001000*')
IDL> dim = size(data,/dimension)
IDL> nx=dim[0] & ny=dim[1] & nd=dim[2]
IDL> xax = (findgen(nx)-0.5) ;; x軸
IDL> yax = (findgen(ny)-0.5) ;; y軸
IDL> img = image(data[*,*,10],xax,yax,axis_style=2,$
IDL              xtickdir=1,ytickdir=1,rgb_table=33)

imageで２次元配列データを画像化し、colorbarでカラーバーを指定の場所に配置します。すると

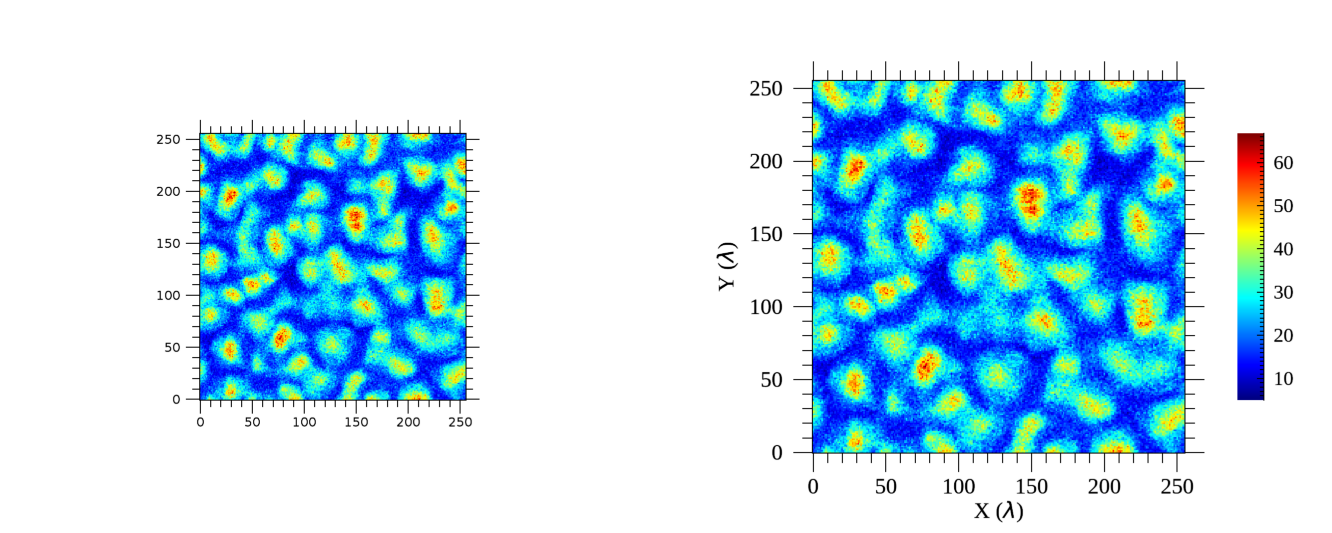
2次元カラー図の例。左が修正前、右が修正後。

これでは画像が小さいので拡大、フォント名・サイズを変更、軸にタイトルを付け加え見栄え良くします。

IDL> img.font_name='Times'
IDL> img.font_size='16'
IDL> img.xtitle='$X (\lambda)$' ;;CAN USE LATEX COMMANDS FOR TITLE
IDL> img.ytitle='$Y (\lambda)$'
IDL> img.xstyle=1
IDL> img.ystyle=1
IDL> img.scale,1.4,1.4 ;; ENLARGE IF IMAGE IS SMALL
IDL> cb  = colorbar(target=img,/orientation,/tickdir,/textpos)
IDL> cb.font_name='Times'
IDL> cb.font_size='14'

これらの属性の修正は、関数の引数として最初から渡すことも可能です。その他の応用は、サンプルプロシージャ md_shock/batch.pro, md_mrx/batch.pro をご覧ください。また、image、colorbar関数に関する情報は

IDL> ?image
IDL> ?colorbar

とすることで、ブラウザで見ることができます。

ベクトル図

ベクトル場を矢印で表現することも可能です。例えば、上記で作成した2次元 カラーマップ図 に速度場ベクトルを付け加える場合は、

IDL> vct = vector(data[*,*,6],data[*,*,7],xax,yax,/overplot)

のようにします（単体で表示する場合はoverplotオプションを外す）。

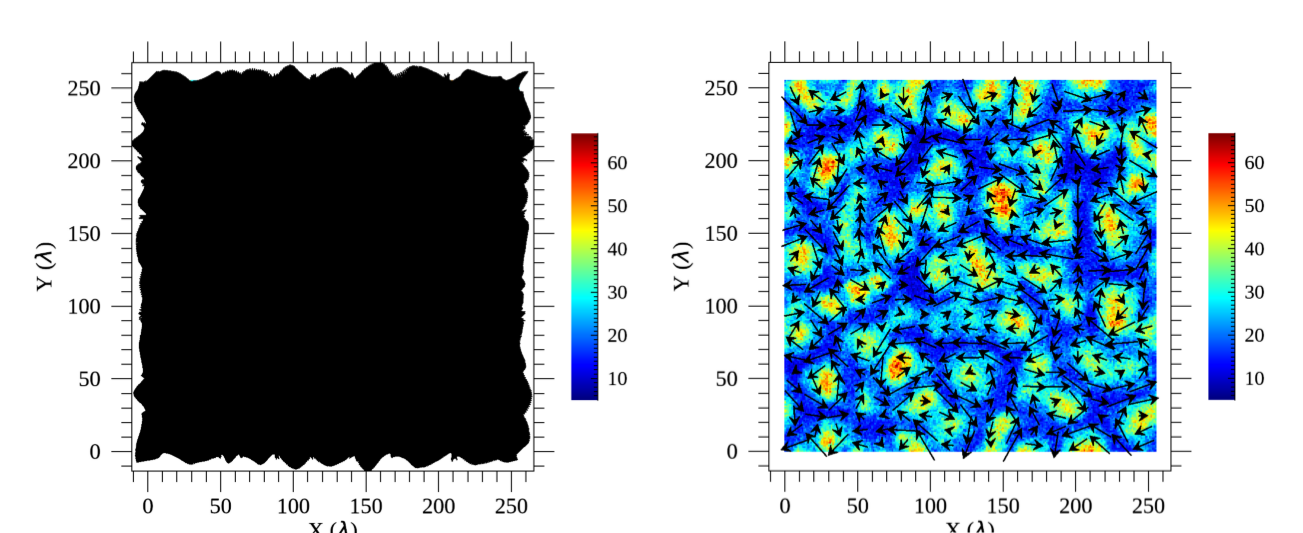
2次元カラーマップ図+速度場ベクトルの例。左が修正前、右が修正後。

しかし、そのままだと全ての情報を矢印で描くことになってしまうので、サンプリングして描画するように修正する。

IDL> vct.x_subsample = 15
IDL> vct.y_subsample = 10
IDL> vct.transparency = 50 ;; ついでに矢印を透過（50%）

その他の応用は、サンプルプロシージャ md_kh/batch.proをご覧ください。また、vector関数に関する情報は

IDL> ?vector

とすることで、ブラウザで見ることができます。

等高線図

磁力線を描く（ベクトルポテンシャルの等高線）ためには、等高線を図示するのが便利です。例えば、上記で作成した2次元 カラーマップ図 に質量密度の等高線を描き加える（この例では圧力分布とほぼ同じ）場合は、

IDL> img.setdata,data[*,*,6],xax,yax ;; 表示する物理量の変更
IDL> cnt = contour(data[*,*,6],xax,yax,/overplot,c_color=0)

のようにして行います。

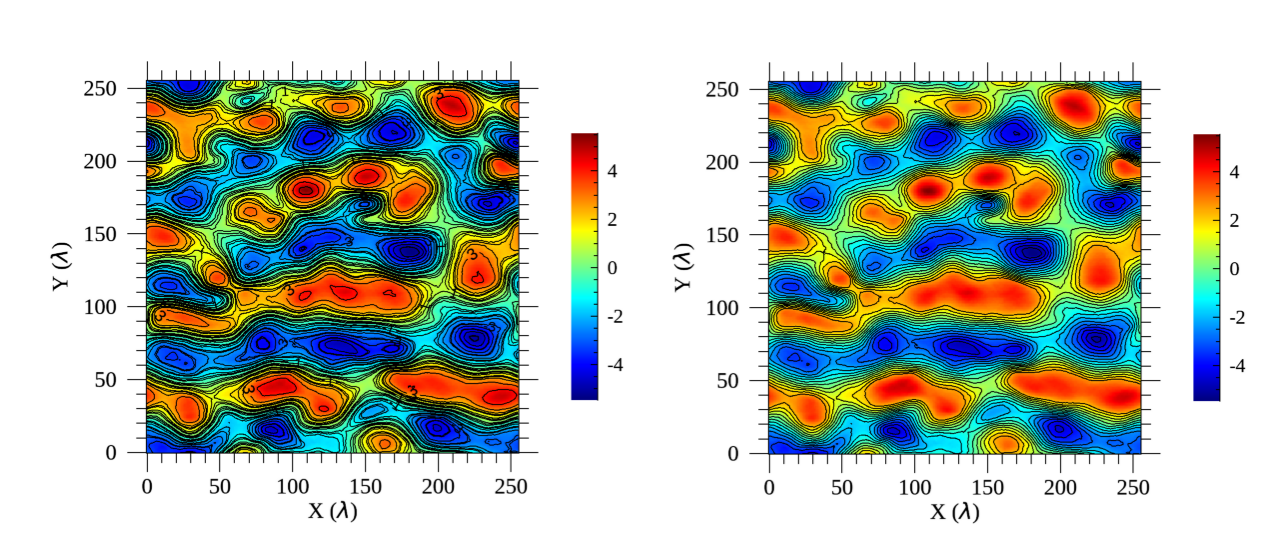
2次元カラーマップ図+等高線の例。左が修正前、右が修正後。

等高線ラベルを削除、等高線の数を増やす場合は、

IDL> cnt.c_label_show=0
IDL> cnt.n_levels=15

のようにして後から修正ができます（関数に引数として渡すことも可能）。contour関数に関する情報は

IDL> ?contour

とすることで、ブラウザで見ることができます。

ベクトル場の流線

ベクトルデータから流線を描くには、以下の共通プロシージャが利用できます。

field_lines_2d.pro

Name
  field_lines_2d
    ２次元のベクトル量から流線（磁力線）を描く

Syntax
  fl = field_lines_2d(ux, uy, [npos=npos,] [nsteps=nsteps,] [len=len,]
                      [r0=r0,] [dir=dir])

Return Value
  fl
    描く流（磁力）線の２次元座標情報。位置を各方向のグリッド数で規格化。

Arguments
  ux, uy
    描画する２次元ベクトル量

Keywords
  npos
    線の数。デフォルトは100。

  nsteps
    トレースするステップ数。デフォルトは10000。

  len
    各方向１ステップあたりの長さ（グリッド単位）を指定する2次元配列

  r0
    各線のスタート位置（x、y）。与えられなければ、ランダムに決められる。
    r0=r0[2,npos]である必要がある。

  dir
    トレースする方向。+1ならばベクトルの向き。-1ならば反対向き。デフォルトは+1。

Example
  IDL> img = image(data[*,*,10],x-dx/2.,y-dy/2.,axis_style=2,$
  IDL>             xtickdir=1,ytickdir=1,rgb_table=33)
  IDL> npos=10 ;; Number of starting points
  IDL> fl=field_lines_2d(data[*,*,6],data[*,*,7],npos=npos)
  IDL> .run
  - for k=0,npos-1 do begin
  - pl = plot(fl[0,*,*,k],fl[1,*,*,k],/overplot,color='black')
  - endfor
  - end
  IDL>

フーリエ変換

現象の発展に伴ってどのようなモードが成長しているのかを把握するためには、フーリエ変換を行います。 1次元データと2次元データをフーリエ変換する共通プロシージャを用意しています。

fftf.pro

Name
  fftf
    1次元データをフーリエ変換し、振動数や波数に対して昇順にソートする。

Syntax
  f1d = fftf(data, time, direction, freq=freq)

Return Value
  f1d
    入力された1次元データ data のフーリエ変換。振動数や波数に対して昇順にソートされている。
    関数の平方の総和（積分）が、そのフーリエ変換の平方の総和（積分）と等しくなるように規格
    化されている（パーセバルの定理）。

  freq
    独立変数 time に対応する振動数や波数が出力される。2$\pi$が掛かっていないことに注意。

Arguments
  data
    1次元データ。

  time
    時刻や座標といった独立変数。

  direction
    フーリエ変換の方向。-1ならフーリエ変換、+1なら逆変換。指定しない場合は-1。

Example
  IDL> data = randomu(systime(/sec), 512)
  IDL> time = findgen(512)
  IDL> f1d = fftf(data, time, freq=freq)
  IDL> plot, freq, abs(f1d), /yl

fft2d.pro

Name
  fft2d
    2次元データをフーリエ変換し、振動数や波数に対して昇順にソートする。

Syntax
  f2d = fft2d(data, x, t, direction, wnum=wnum, freq=freq)

Return Value
  f2d
    入力された2次元データ data のフーリエ変換。振動数や波数に対して昇順にソートされている。
    関数の平方の総和（積分）が、そのフーリエ変換の平方の総和（積分）と等しくなるように規格
    化されている（パーセバルの定理）。

  wnum
    独立変数 x に対応する振動数や波数。2$\pi$が掛かっていないことに注意。

  freq
    独立変数 t に対応する振動数や波数。2$\pi$が掛かっていないことに注意。

Arguments
  data
    2次元データ。

  x, t
    時刻や座標といった独立変数。

  direction
    フーリエ変換の方向。-1ならフーリエ変換、+1なら逆変換。指定しない場合は-1。

Example
  IDL> data = randomu(systime(/sec), 128, 128)
  IDL> x = findgen(128)
  IDL> t = findgen(128)
  IDL> f2d = fft2d(data, x, t, wnum=wnum, freq=freq)
  IDL> plot_clcnt, alog10(abs(f2d)), xax=wnum, yax=freq

２次元頻度分布

粒子計算において、粒子の速度分布関数を得ることは物理を議論する上で有用です。２次元の頻度分布を計算する共通プロシージャを用意しています。

psd_calc.pro

Name
  psd_calc
  ２次元の頻度分布を計算する。

Syntax
  psd_calc, psd, xax, yax, data1, data2, [max_x=max_x,] [min_x=min_x,]
            [max_y=max_y,] [min_y=min_y,] [nbin_x=nbin_x,] [nbin_y=nbin_y]

Return Value
  psd
    出現頻度数

  xax, yax
    各ビンの値を表す

Arguments
  data1, data2
    頻度を求める元データ

Keywords
  max(min)_x
    1次元目のデータの最大（最小）値を設定する

  max(min)_y
    2次元目のデータの最大（最小）値を設定する

  nbin_x(y)
    1（2）次元目のビンの数を指定する

サンプルプロシージャ

IDLによる可視化のサンプルプロシージャ batch.pro が課題ディレクトリ "$PCANS_DIR/em1d/md_wave/", "$PCANS_DIR/em1d/md_shock/" , "$PCANS_DIR/em1d/md_whistler/" , $PCANS_DIR/em2d/md_shock/ , "$PCANS_DIR/em1d/md_mrx/" にありますので、適宜修正してお使いください。 batch.proは

IDL> .run batch

で実行し、書かれている内容をバッチ処理します。

アニメーションの作り方

以下の様に、IDL上で結果をpngファイルとして保存します。

IDL> deni = file_read('*_den_i.dat')
IDL> dim = size(deni)
IDL> nx=dim[0] & ny=dim[1] & nt=dim[2]
IDL> xax = findgen(nx)-0.5 & yax = findgen(ny)-0.5
IDL>.run
- for i=0,nt-1 do begin
- if(i eq 0)then begin
- img = image(deni[*,*,i],xax,yax,axis_style=2,$
-             xtickdir=1,ytickdir=1,rgb_table=33)
- endif else begin
- img.setdata,deni[*,*,i]
- endelse
- img.save,'result'+strcompress(string(i,format='(i3.3)'),/remove)+'.png'
- endfor
- end

上記のようにすると、作業ディレクトリには"result005.png"のように連番でファイル名が付けられた画像ファイルが作成されます。

結果をpngファイルに出力後、LinuxにインストールされているImagemagick (convert)やffmpegを使って、結果の図をアニメーション化します。まず、convertを使った方法を説明します。

$ convert result???.png result.gif

のようにすると、gifアニメーションが作成されます。convertの際の詳しいオプションは"man convert"に委ねます。

次に、ffmpegを使ったアニメーション作成例を示します。

$ ffmpeg -i result%03d.png -sameq -vcodec mjpeg result.avi

のように、gifアニメーション以外のフォーマット（この例では、元の画像と同じ画質で、エンコードにmjpeg、格納形式としてaviを指定している）の動画ファイルが作成可能です。更なるオプションは"man ffmpeg"に委ねます。

上記の様に、IDL上での結果を連番で名前を付けた画像ファイルに保存すれば、Windows, Mac-OSでのその他のツールも利用可能だと思います。