研究内容

1.研究目的


２つの天体が、互いに引力を及ぼしあい、共通重心の周りを公転しているような系を考える。

実際の例としては、地球と月、あるいは縮退星を含んだ連星等があるが、今回の研究は、２つの恒星からなる近接連星、あるいは一方が縮退星であるような近接連星があった場合に、２つの星の周りの任意のガス粒子がどのような運動をするかをシミュレーションしようというものである。

これにより、縮退星の周りに降着円盤が形成される様子や、このような系で角運動量がどのように変化するのかといったことがわかる。（かもしれない。）
 
 

2.ロシュポテンシャル（Roche Potentials)


連星系を構成する両星の質量をｍ１，ｍ２（ｍ１＞ｍ２）、星間距離をA、両星が向かい合ったまま公転するとして、ケプラー角速度をωとする。

ｍ１星の重心に原点をとり、両星の重心を結ぶ線をｘ軸、軌道面内にｙ軸、軌道面に垂直方向にｚ軸の直交座標系をとると、任意の点Ｐ（ｘ、ｙ、ｚ）に働く両星からの引力と遠心力とによる全ポテンシャルΨは次式で示され、これをロシュポテンシャル（Roche Potentials)とよぶ。
 
 

（式１）

ここで、ｒ１はｍ１星からの、ｒ２はｍ２星からの点Ｐの距離であり、
 
 






となる。また、ケプラー角速度ωは、

であたえられる。
 

３．数値計算


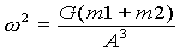
今回の計算では、簡単にするため、まずｚ座標を無視し、ｘｙ平面内に限って見ることにした。
また、式１で、G=A=ω=1、ｑ＝ｍ２／ｍ１として、式２を得、ロシュ等ポテンシャルの図を描いた。
 
 
 

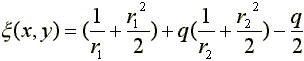（式２）


 

図はそれぞれ、q=0.5、q=0.01、q=0.001のときのロシュ等ポテンシャルを表している。

図の中に赤字で示されているのはラグランジュ点（Lagrange point)というもので、この点上で、すべての力が釣り合う。２つの星からなる連星の周りにはこの点が必ず５つあり、このうちＬ４点とＬ５点は周辺で一番ポテンシャル値の低い安定点である。よって月と地球の場合にはこの点上にスペースコロニーを建設するらしい。図中で８の字を描いている等ポテンシャル面を内部ロシュローブ（inner Roche lobe）、Ｌ２点を含み亜鈴状に閉じた等ポテンシャル面を外部ロシェローブ(outer Roche lobe)と呼ぶ。

次に、質量０の質点にかかる力を連星の公転周期で回転する座標系に乗って考え、数値計算を行う。

ここで質量０の質点とは、粒子が両星に何の影響も与えないということで、このような場合を「制限三体問題」という。連星の公転周期で回転する座標系に乗って考えると、式２よりｘ方向、ｙ方向の運動方程式がそれぞれコリオリ力の項を含んだ次式であたえられる。
 
 





上の２つの式を元に、ルンゲクッタ法による数値計算のプログラム（santai.c）をつくり、質点に初期位置を与え、時間変化のシミュレーションを行った。
 
 

４．結果


シミュレーションはすべて、ｑ＝０．５、すなわち両星の質量比２：１の場合で行った。最初に質点を置く場所は、
 

１．一方の星からもう一方の星にガスが降着する場合に通ると思われるＬ１点付近。
２．ガスが完全に外部ロシュローブを満たした後、外に漏れだすときに通ると思われるＬ２点付近。
３．Ｌ３点付近
４，安定点であるＬ４、Ｌ５点付近
 

とした。（それぞれの結果は上をクリックすると見られます。）
得られた結果から言えることとして、
 

・Ｌ１点からあふれ出たガス粒子はもう一つの星の引力にとらえられ、周りをまわる。このような粒子が降着円盤を形成すると考えられる。

・Ｌ２点からあふれ出た粒子は回転系から見ると、連星の回転方向とは逆向きに渦を描いて流出していく。これにより連星系の角運動量が失われる。