1次元コード

1次元コードはシリアル計算コードのみで、以下のような構成になっています。

Makefileは本1次元コードのバイナリ生成、削除をコントロールしています。初期化するには$PCANS_DIR/em1d内で、

$ make clean

としてください。Makefile_incには、

FC = gfortran
FFLAGS = -O2

が記述されており、makeする際の環境変数が設定されています。ここでは、"$FC"にはFortranコンパイラ、"$FFLAGS"にはコンパイラオプションが設定されています。コンパイラとコンパイラオプションを変更したい場合は、例えば、

FC = ifort
FFLAGS = -O3

のように修正してください。

シリアル版では、物理課題として「 線形波動 (md_wave) 」、「 電子２流体不安定（md_ebeam） 」、「 イオンサイクロトロン不安定（md_ibeam） 」、「 電子温度異方性不安定 (md_whistler） 」、「 衝撃波 (md_shock） 」が用意されています（2018年8月現在）。各課題には、

が含まれており、それぞれの課題に沿った初期設定のサンプルが置かれています。"dat/"は計算結果の出力先で、電磁場と粒子データが出力されます。"mom/"は"dat/"内にある粒子データを元にモーメント計算をした時の出力先です。"psd/"には"dat/"にあるデータから粒子の位置、速度がASCII形式で出力されます。

注意

全ての粒子の情報がASCII形式で出力されるので、psd内のデータは非常に大きな物になります。HDDの容量にご注意ください。

例えば、衝撃波の計算を行うには、

$ cd $PCANS_DIR/em1d/md_shock
$ make
$ ./a.out

とします。リスタートに必要な途中の計算データは（粒子、電磁場、時刻）はFortran Unformatted形式で"dat/"内に出力されます。また、モーメントデータ・粒子の位相空間情報はそれぞれASCII形式で、"mom/", "psd/"内に出力されます。"psd/"内のデータ使うことで、分布関数を求めることができます。

パラメタ設定

各課題に含まれる"const.f90"では、シミュレーションの実行に必要なパラメタ定数があらかじめ設定されています。本ファイルを編集することで、違うパラメタの計算を行うことができます。以下では衝撃波の課題（md_shock)を例に説明します。

const.f90:

module const

  implicit none

!!************************ NUMERICAL CONSTANTS ***********************************!!
  integer, parameter :: nx  = 2048  ! NUMBER OF GRID POINTS
  integer, parameter :: np  = 500   ! NUMBER OF PARTICLES IN EACH CELL
  integer, parameter :: nsp = 2     ! NUMBER OF PARTICLE SPECIES
  integer, parameter :: bc  = -1    ! BOUNDARY CONDITION (PERIODIC:0, REFLECTIVE:-1)

!! SETUP FOR SUBROUTINES CALLED IN MAIN PROGRAM
  integer, parameter :: itmax  = 40000 !NUMBER OF ITERATION
  integer            :: it0    = 0     !0:INITIAL, NONZERO/9999999: RESTART DATA
  integer, parameter :: intvl1 = 5000  !INTERVAL FOR PARTICLES & FIELDS STORAGE
  integer, parameter :: intvl3 = 1000  !INTERVAL FOR RECORDING MOMENT & FIELDS DATA
  integer, parameter :: intvl4 = 1000  !INTERVAL FOR RECORDING PSD DATA
  character(len=128) :: dir    = './dat/' !DIRECTORY FOR OUTPUT
  character(len=128) :: dir_mom= './mom/' !DIRECTORY FOR MOMENT DATA
  character(len=128) :: dir_psd= './psd/' !DIRECTORY FOR MOMENT DATA
  character(len=128) :: file9  = 'init_param.dat' !FILE NAME OF INIT CONDITIONS
  character(len=128) :: file10 = 'file10.dat' !FILE NAME OF PARTICLE DATA

!! OTHER CONSTANTS
  real(8), parameter :: gfac   = 0.501D0 !IMPLICITNESS FACTOR > 0.5
  real(8), parameter :: cfl    = 0.5D0   !CFL CONDITION FOR LIGHT WAVE
  real(8), parameter :: rdbl   = 1.0D0   !DEBYE LENGTH / CELL WIDTH
  real(8), parameter :: pi     = 4.0D0*atan(1.0D0)

!!************************ PHYSICAL CONSTANTS ***********************************!!
!!      n0 : NUMBER OF PARTICLES/CELL IN THE UPSTREAM REGION
!!     vte : ELECTRON THERMAL SPEED
!!     fpe : ELECTRON PLASMA FREQUENCY
!!   rmass : ION-TO-ELECTRON MASS RATIO
!!   sigma : (WGE/WPE)**2
!!   beta? : PLASMA BETA FOR ION AND ELECTRON
!!   Ma    : MACH NUMBER OF THE FLOW (IN THE SIMULATION FRAME)
!!   theta : UPSTREAM MAGNETIC FIELD ANGLE NORMAL TO THE X AXIS
!!   lbuf  : INITIAL BUFFER WITHIN WHICH FLOW SMOOTHLY DECREASES TO ZERO
  integer, parameter :: n0    = 64
  real(8), parameter :: vte   = 1.0D0
  real(8), parameter :: fpe   = 1.0D0
  real(8), parameter :: rmass = 25.0D0
  real(8), parameter :: sigma = 0.04D0
  real(8), parameter :: betae = 0.5D0, betai = 0.125D0
  real(8), parameter :: ma    = 3.0
  real(8), parameter :: theta = 90.0/180.0*pi
  real(8), parameter :: lbuf  = 500.0

end module

最初は、数値計算に必要なパラメタを設定しています。nxはグリッド数、npは予想されるセル内の粒子数の最大値、nspは粒子種数で通常はイオンー電子系なので、nsp=2とします。bcは境界条件を指定するもので、 pCANS では周期境界（bc=0）と反射端（bc=-1）が選べます。

続いて、ステップ数、出力先などが設定されています。各パラメタは上コメントに記述されています。"gfac"は、電磁場を陰解法で解くときのimplicit factorで、通常0.5より少し大きな値が設定されます。"it0"はステップ数のベースカウンタで、"it0=0"の時は最初から計算します。途中から計算を再開する時には、再開する時間ステップ数の値を設定します。

ファイルの後半では各物理課題に沿った物理定数（コメント内に詳述）が設定されています。n0は初期に配置するセルあたりの粒子数ですが、系の時間発展中にnpを越えないように注意してください。

モーメント計算と粒子位相空間情報

"const.f90"内で設定されているintvl3, intvl4では、それぞれモーメント計算結果、粒子の位相空間情報を出力する時間感覚を設定しています。それぞれ"dir_mom", "dir_psd"で指定したディレクトリ内に出力されます。

モーメント計算は、密度（0次モーメント）、

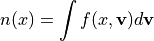
速度（1次モーメント）、

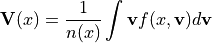
温度（2次モーメント）、

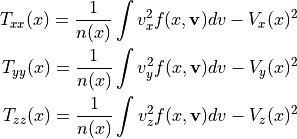
に従って計算します。